大家好,工行纸白银价格走势曲线图(工行纸白银k线走势小编来为大家解答。呢,很多朋友还不理解,现在让我们一起来介绍下,希望能帮助到你!大家好。今天给大家分享一些关于工行纸银k线走势的知识,也会讲解一下工行纸银价格走势的
2023-12-19 01:50:02
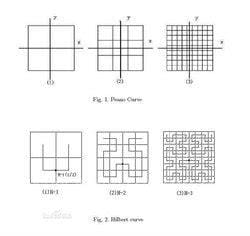
1890年,意大利数学家皮亚诺发明了一条可以填充正方形的曲线,它被称为皮亚诺曲线。后来希尔伯特做出了这条曲线,也叫希尔伯特曲线。
希尔伯特-皮亚诺曲线是一种分形图形,可以画得无限复杂。它的初始图元是一个正方形,在迭代生成的过程中,不断细化小正方形。图中的线段实际上是连接正方形的线。其特点是迂回曲折,一气呵成,可以通过平面上一个正方形区域内的所有点。希尔伯特曲线是一条奇妙的曲线。只要函数选择得当,就能画出连续的参数曲线。当参数t在0和1的范围内时,曲线将遍历单位正方形内的所有点,得到一条充满空间的曲线。希尔伯特曲线是一条连续的非导数曲线。
Peano曲线是一个曲线序列的极限,是一条可以填充正方形的曲线,peano曲线是一条不可微的曲线,在数学上有一定的应用,因为一般情况下,一维的直线不能填充二维的正方形,但是peano曲线解决了这个问题,说明我们对维数的理解是有缺陷的,需要重新审视维数的定义。这就是分形几何的问题。在分形几何中,维数可以是一个叫做分形维数的分数。这个结论的证实,让我们不得不重新认识维度在数学中的应用,这也是数学知识的神奇之处。除了皮亚诺曲线,数学中还有很多神奇的结论,这些结论的存在说明了数学知识的神奇。本文将为大家详细介绍。
皮亚诺曲线怎么画?有什么等式吗?
有人知道皮亚诺曲线是怎么画出来的吗?最近看到一个叫peano curve的设计,很惊艳。世界上还有这样神秘的设计。网上查了才知道叫皮亚诺曲线。皮亚诺曲线怎么画?这是数学的神奇结论。
皮亚诺曲线有解析式吗?
皮亚诺曲线能用解析式表示吗?如果没有,我想问有没有可以用解析式表示的函数?谢谢大家。
解析:(1)钢琴曲线没有解析式(2)y =[x2]的图像。
皮亚诺曲线
Peano曲线是一个曲线序列的极限,是一条可以填充正方形的曲线,peano曲线是一条不可微的曲线,在数学上有一定的应用,因为一般情况下,一维的直线不能填充二维的正方形,但是peano曲线解决了这个问题,说明我们对维数的理解是有缺陷的,需要重新审视维数的定义。这就是分形几何的问题。在分形几何中,维数可以是一个叫做分形维数的分数。这个结论的证实,让我们不得不重新认识维度在数学中的应用,这也是数学知识的神奇之处。除了皮亚诺曲线,数学中还有很多神奇的结论,这些结论的存在说明了数学知识的神奇。本文将为大家详细介绍。
数学定理的魔力
学过数学的人都应该知道,数学对某些人来说是非常神奇的,因为很多人无法理解数学的神奇,但数学的魅力是不可磨灭的。而对于一些数学曲线,如果按照特定的数学规律进行计算,就能很好地展现出神奇的曲线特征,如双曲线、皮亚诺曲线、阿基米德螺线等。,都是数学定理计算下的特性曲线。
皮亚诺曲线的观点在哪里?
1890年,意大利数学家皮亚诺发明了一条可以填充正方形的曲线,它被称为皮亚诺曲线。皮亚诺对区间[0,1]上的点和正方形上的点之间的对应关系给出了详细的数学描述。其实对于t∈[0,1],正方形的这些点可以指定两个连续函数,x=f(t)和y=g(t),这样x和y取属于单位正方形的每一个值。后来希尔伯特做出了这条曲线。
“1872年,康托尔在一篇文章中专门用了一章来讨论实数,尤其是无理数。他给自己定下了一个目标:在不预设无理数存在的前提下,建立一个令人满意的无理数理论。显然,所有有理数的集合为此提供了基础。康托尔用一个无穷序列的有理数来定义无理数及其序列关系。从集合论的角度来看,因为数列对应的是数的集合,而不是元素本身,所以即使只有一个元素的数列也应该对应一个数的集合。上面的有理数定义很明显构造了一个包含自指的集合:数A等于一个集合,这个集合中有一个元素,就是数A本身。这样的一套包含了罗素悖论。
需要明确的一点是,无穷数列的构造过程与取无穷数列极限的过程之间的关系。我们已经知道区间[0,1]上有无数个有理数,我们可以用一个递归的无穷过程来生成这些有理数。区间[0,1]中的无理数都是有理数集合的极限点。但是有理数的集合和无理数的集合是明显不同的。也就是说,构造有理数集的无限过程不包括取极限的过程,不能认为取极限的过程一定包含在无限过程中。否则,根据第一节,无理数的定义将包括罗素悖论。事实上,很多声称找到了实数可数证据的例子,都犯了这样的错误,认为无穷过程一定包含极限过程。
另外,可以用反证法证明希尔伯特曲线并没有建立曲线到平面的一一对应关系。假设曲线的坐标区间为[0,1](即假设曲线的长度为1),对于正方形中线Y轴上的一个点P,曲线上的数X属于[0,1]并映射到点P,由于希尔伯特曲线是左右对称的,所以可以立即得到数(1-x)也映射到P点。因为这种映射是一一对应的,所以有x=1-x=1/2,即1/2对应Y轴上的一条线段,这就与之前的一一对应的假设相矛盾。
这种观点指出,在康托尔用有理数的基本序列定义实数中,实数域中的一个有理数A等于定义的序列,这实际上构造了一个包含自指的集合:数A等于一个集合,这个集合中有一个元素,就是数A本身。这样的一套包含了罗素悖论。本文还分析了peano曲线等一维到二维映射的例子,指出它们实际上包含了上述悖论。
相关文章
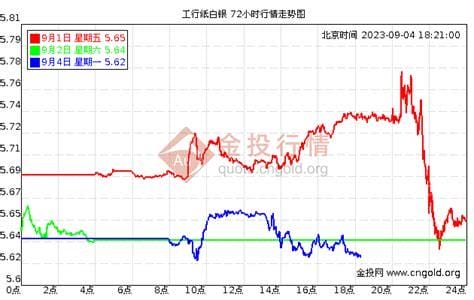
大家好,工行纸白银价格走势曲线图(工行纸白银k线走势小编来为大家解答。呢,很多朋友还不理解,现在让我们一起来介绍下,希望能帮助到你!大家好。今天给大家分享一些关于工行纸银k线走势的知识,也会讲解一下工行纸银价格走势的
2023-12-19 01:50:02

生活中有许多的朋友最近问小编A处处吻全程拉丝伸舌头的问题,那小编收集整合后,今天为大家分享关于的相关文章,一起来了解一下吧!摘要:初吻是一个抽丝吐舌的动作,有着独特的魅力和亲切感。本文将从三个方面来阐述这个动作的
2023-10-29 02:09:01

唐江山事件已经破解希望不清楚的大家在这看一看,小编已经为大家把这个问题总结好了,希望接下来的能帮大家解决这个问题,看完了记得分享哦!“脱胎换骨”这个词大家都很熟悉。意味着一个人有前世的记忆。说到重生,就不得不谈
2023-10-13 14:44:52

有些小伙伴经常会碰到什么是悲伤的双曲线啊的问题,但是对于不是非常了解,给小伙伴带来了很多困惑,但小伙伴们找到这里算是没白来,因为小编就带大家详细讲解一下,具体内容如下。首先,我想解释一下悲伤是什么意思:悲伤、难过
2023-10-13 10:34:55
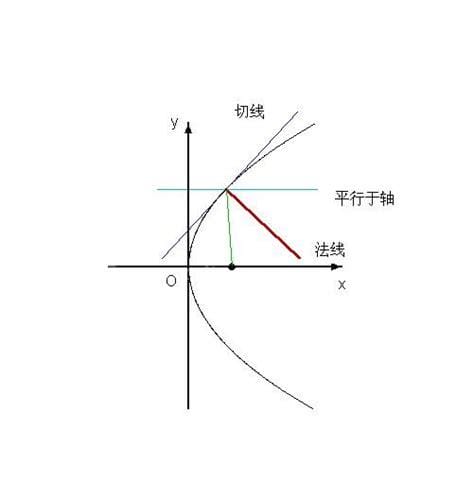
如何求曲线的法线方程是各位朋友所需要解决的问题,问题理解之后可以给朋友带来很大的帮助,所以今天小编就给大家带来的详细讲解,一起来看看吧。首先通过求导得到切线斜率,然后根据点歪斜得到曲线的切线方程。然后利用斜率
2023-10-12 19:13:02