生活的过程中,小伙伴们是不是经常遇到一些很困惑的问题,比如我们今天要说的excel减法函数公式是什么这个问题,要解决这样的问题其实很简单,下面可以跟着小编来具体了解一下吧。在excel中,减法的作用是:IMSUB函数。公式是:A
2024-03-14 22:42:02
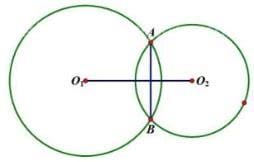
弦长的一般公式
│x1-x2 │√( k2+1)=│y1-y2│√[(1/k2)+1]其中k是直线的斜率,(x1,y1)和(x2,y2)是直线和曲线的两个交点。
常见弦长公式的求解
两个圆的半径,在相交的情况下,两个圆心的距离是背。
假设两个半径为A和B,中心距为c。
那么公共弦的长度是。
(a+b+c) (a+b-c) (a+c-b)和(b+c-a)的乘积有根号,然后除以c。
具体推导过程只是解方程,可以自己推。
两个圆相交时中心距的关系。
1.当两个圆刚好相交并且有两个交点时,中心距离A必须小于半径之和。
2.两个圆相交到一定程度,此时两个圆心在同一个圆上。连接两个圆心和两个圆的交点会形成一个三角形。边长r+a > r = a > r-r
设两个圆分别为
x^2+y^2+c1x+d1y+e1=0①
x^2+y^2+c2x+d2y+e2=0②
减去这两个表达式
(x^2+y^2+c1x+d1y+e1)-(x^2+y^2+c2x+d2y+e2)=0③
③是弦所在直线的方程。
先证明这条直线穿过两个圆的交点。
设交点为(x0,y0),满足① ②。
所以交点在直线③上。
因为只有一条直线通过两个交点,所以可以根据两个交点的长度求出两个圆的交点的公弦长。
发展
椭圆弦长公式
│x1-x2│ √ (1+k)
设直线y=kx+b
代入椭圆圆的方程,可以得到:x/a+(kx+b)/b = 1。
设两个交点为A和B,A点为(x1,y1),B点为(x2,y2)。
那么ab = √ [(x1-x2)+(y1-y2)]
分别代入y1=kx1+b.y2=kx2+b。
然后是
AB=√ [(x1-x2) +(kx1-kx2)
=√ [(x1-x2) +k (x1-x2) ]
=│x1-x2│ √ (1+k)
同样可以证明弦长= │ y1-y2 │√ [(1/k)+1]。
直线:Ax+By+C=0
椭圆:x ^ 2/a ^ 2+y ^ 2/b ^ 2 = 1。
求一条直线和一个椭圆的交点
(b^2+(a^2*a^2)/b^2)*y^2+2*b*c*y+c^2-a^2*a^2=0
设m = (b 2+(a 2 * a 2)/b 2)
n=2*B*C
p=C^2-A^2*a^2
设m1 = (a 2+(b 2 * b 2)/a 2)
n1 = 2 *交流电
p1=C^2-B^2*b^2
得到y = (-n √ (b 2-4 * m * p))/2 * m。
当y =(-n-√( B2-4 * m * p))/2 * m;x=(-n1-√(b1^2-4*m1*p1))/2*m1
当y =(-n+√( B2-4 * m * p))/2 * m;x=(-n1+√(b1^2-4*m1*p1))/2*m1
椭圆弦长公式是一个数学公式。直线与圆锥曲线相交求弦长的一般方法是将直线y=kx+b代入曲线方程,化为关于x(或关于y)的二次方程,设定交点坐标,利用维耶塔定理和弦长公式√ (1+k2) [(x1+x2) 2-4 x1 x2]求弦长。
相关文章
生活的过程中,小伙伴们是不是经常遇到一些很困惑的问题,比如我们今天要说的excel减法函数公式是什么这个问题,要解决这样的问题其实很简单,下面可以跟着小编来具体了解一下吧。在excel中,减法的作用是:IMSUB函数。公式是:A
2024-03-14 22:42:02
最近很多朋友都遇到了word里面怎么求和公式的问题,今天小编就来为大家解答,快来看看吧。【div】【/div】word文档中的求和运算方法如下:1.首先,用word打开文档,找到要求和的表格。2.将光标放在sum值所在的单元格中,然后单
2024-03-14 11:06:01
有许多朋友最近问小编word里插入公式显示不全的问题,那么小编收集整合后,今天为大家分享关于的解答,一起来了解一下吧!首先,选择无法在word2010中完整显示的公式,如图所示。然后选择开始选项卡并单击段落右下角的45度箭头,如
2024-03-11 22:18:02
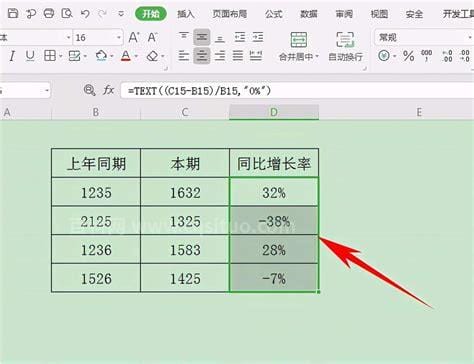
大家在生活的过程中总会遇到一些问题,比如同比的计算公式,那么今天小编就为大家分享关于的相关文章,希望在这篇文章中你能了解到相关内容。计算公式:同比增长率=(期数-期数)÷期数×100%。某个指标的同比增长率=(当前某个
2024-03-10 04:24:01
excel函数if公式怎么用?希望不清楚的大家在这看一看,小编已经为大家把这个问题总结好了,希望接下来的能帮大家解决这个问题,看完了记得分享哦!边肖通过一个简单的例子告诉你如何使用if公式!假设数据在A1输入,在B1判断。如果
2024-03-10 03:42:02