ln1为什么等于0

大家在生活的过程中会遇到很多问题，比如有些小伙伴对ln1为什么等于0不是很懂，不过没有关系，小编今天就给大家详细讲解一下这个问题，具体内容如下。

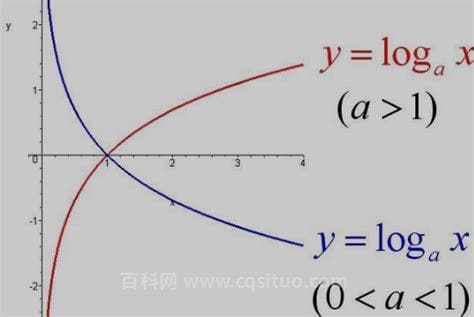
在物理学、生物学等自然科学中具有重要意义。一般的表示方法是lnx。Logx在数学中也常用来表示自然对数。因为对数函数的基本性质通过不动点(1，0)，也就是当x=1，y=0时，所以ln1等于0。

A = b (a > 0且a≠1)，n = logab (a > 0，a≠1)。

若a = b (a > 0，且a≠1)，称为a的n次方等于b，这里a称为底数，n称为指数，b称为带底数的n次方。

如果写成对数形式，就是:n = logab (a > 0，a≠1)。

这里a还是叫底数，b叫实数，n叫b带底数的对数。

可以看出，指数和对数都是n，即指的是同一个东西，只是在不同的场合有不同的称呼。

对数算法

1、log(a)(M ^ N)= log(a)M+log(a)N

2、log(a) (M÷N)=log(a) M-log(a) N

日志(M^n=nlog(a)

4、log(a)b*log(b)a=1

log(a) b=log (c) b÷log (c) a

指数运算

1.[a m]×[a n]= a(m+n)[同底数乘方，常数底数，指数加法]

2.[a m]⊙[a n]= a(m-n)[同底数乘方除法，常数底数，指数减法]

3.[A m]n = A(Mn)[幂的幂，常数基数，指数乘法]

4.[AB]m =(A m)×(A m)[乘积的幂等于各因子的幂，再乘以得到的幂]

扩展数据

1.特别地，我们把以10为底的对数称为常用对数，记为lgN。

2.以无理数e(e=2.71828…)为底数的对数称为自然对数，记为lnN。

3.零没有对数。在实数范围内，负数没有对数。在虚数范围内，负数是对数。

4.e(2k+1)πi+1=0，所以ln(-1)，ln (-1) = (2k+1) π i有多个周期值，这样，任何负数的自然对数都有周期的多个值。比如:ln(-5)=(2k+1)πi+ln 5。