许多朋友不知道房产税计算方法及公式,并且对此很疑惑,那么今天就和小编一起来看看吧,一定可以帮助到你。房产税计算方法及公式 房产税有两种计算方式:首先,从价财产税是基于财产的剩余价值。房产税按照房产原值扣除10%至3
2023-12-27 02:10:02

我写过很多关于欧拉恒等式的文章,可以说是世界上最美的等式了。这篇论文是关于多面体欧拉定理的。每当我开始写一篇关于数学的文章时,我的大脑告诉我,这篇文章是由莱昂哈德·欧拉赞助的。欧拉对几乎所有数学领域都有贡献。
拓扑不变量欧拉特征可能是数学领域第二美的方程。我这么说不是因为我个人喜欢这个方程。事实上,许多科学家更愿意将其视为一个整体。甚至LiveScience杂志的一篇文章在《11个最美的数学方程》中也提到了它。
顶点-边+面= 2,也就是我们熟知的多面体欧拉定理。我们来分析一下。
对于任何凸多面体,顶点数减去边数加上上面的数总是等于2。在进一步分析之前,我们先来看五个柏拉图多面体。
柏拉图多面体在三维空间中,柏拉图的多面体是正凸多面体。它由相等的、规则的和多边形的面组成,每个顶点上有相同数量的面。
四面体有四个面和四个角,由六条边连接。对于四面体,V = 4,E = 6,F = 4。
V-E+F = 4-6+4 = 2,所以满足多面体欧拉定理。
我在下面列出了所有柏拉图的多面体。
四面体:V = 4;E = 6;F = 4。立方体:V = 8;E = 12;F = 6。八面体V = 6;E = 12;F = 8。十二面体:V = 20;E = 30;F = 12。二十面体:V = 12;E = 30;F = 20。五个正多面体。公元前360年的一个温暖的夏夜,柏拉图正坐在沙发上,想着把四种经典元素(土、气、水、火)的每一种都和柏拉图的多面体联系起来。土壤和立方体连接在一起;气有八面体,因为它的微小成分光滑到人几乎感觉不到;水与二十面体相关,因为它流经你的手;火是和四面体联系在一起的,因为火的温度让人感到尖锐刺痛。当然,我不能理解他的解释。
开普勒的宇宙奥秘中元素的任务。快进到16世纪,德国天文学家约翰尼斯·开普勒将太阳系的六颗行星(当时只发现了除地球以外的五颗行星)与这五个柏拉图多面体联系起来(至少试图建立联系)。
1596年,开普勒提出了一个太阳系模型。在这个模型中,五个实体相互嵌入,并被一系列内接和外切的球体分隔开。
开普勒认为可以用代表土星轨道的球体中的五个柏拉图多面体来理解行星之间的距离关系,这是一个很酷的想法。
开普勒的柏拉图多面体太阳系模型。这六个球体分别对应水星、金星、地球、火星、木星和土星。最里面的部分是八面体,然后是二十面体、十二面体、四面体,最后是立方体。
当然开普勒离现实还很远,但是我们不要忘记这五个柏拉图多面体有多重要。回到数学,回到欧拉。
多面体欧拉定理甚至适用于球体。如果考虑所有的经纬线,计算整个地球的顶点、面、边,用多面体欧拉定理公式,会得到2!
现在,我们来看看这个四面体是如何生成一个球体的细分的,其中四面体的顶点、边、面对应于细分后的顶点、边、面,细分有4个顶点、6个边、4个面。多面体欧拉定理适用于四面体。
类似地,立方体产生球体的8个顶点、12个边和6个面的细分。同样的事情也发生在其他柏拉图多面体上。
基本上,从曲面S到曲面S '的任何同胚映射S的一个细分到S '的一个细分,映射S的顶点到S '的顶点,映射S的边到S '的边,映射S的曲面到S '的曲面是一对一的。
在拓扑学中,同胚是两个拓扑空间之间的双连续函数。同胚是拓扑空间范畴中的同构。
我们可以得出这样的结论:细分的欧拉特征在同态下是不变的,因为它遵循VE+F的值..因此,我们也可以说曲面的欧拉特征是拓扑不变的。
对于二维欧拉特性也适用于二维几何。
画一条线。它有2个顶点,1条边和0个面。所以V-E+F = 1。
假设这两个顶点是A和B,在平面上的任意位置放一个顶点C(不在AB边)。画一个边界,BC现在,我们有3个顶点,2条边和0个面。同理,V-E +F = 1。现在,用一条边连接C和A。现在我们有3个顶点,3条边和1个面,V -E+F = 1。
欧拉特征在所有这些情况下都存在。现在假设整张纸是一张脸,除了刚刚得到的三角形,得到V-E+F = 2。
相关文章

许多朋友不知道房产税计算方法及公式,并且对此很疑惑,那么今天就和小编一起来看看吧,一定可以帮助到你。房产税计算方法及公式 房产税有两种计算方式:首先,从价财产税是基于财产的剩余价值。房产税按照房产原值扣除10%至3
2023-12-27 02:10:02

光合作用的公式超级多的小伙伴们都在问小编解决的方法,相信大家看完这篇,有什么区别?听听小编怎么说心中会有答案的,本期的内容都是满满的干货,千万不要错过哦!光合作用的公式 1.总反应:CO2+H2O 18 —→( CH2O)+O218。2.注
2023-12-25 04:30:01
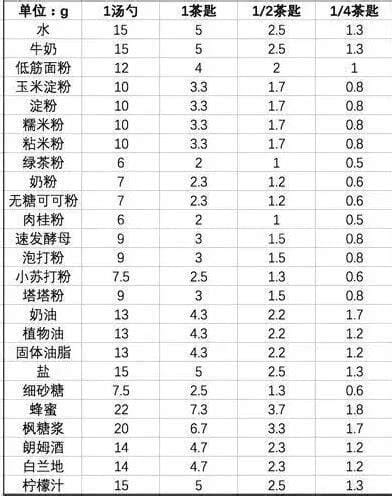
最近毫升跟克怎么换算这个问题很火,不同的人一定有不同的问题,比如许多人都会遇到的,今天小编就来为大家解答,快来看看吧。毫升跟克怎么换算 毫升是液体的体积单位,克是重量单位。两者的转换方法如下。毫升和克的换算必须
2023-12-24 22:10:01

生活中,有很多朋友觉得港币和人民币的汇算率很难弄明白,那么我们到底要如何解决这个问题呢,今天小编就带来大家看看,希望可以帮助各位。本文讲的是港币与人民币的汇率公式,以及港币和人民币的汇算率对应的知识点。希望对你
2023-12-21 08:00:01
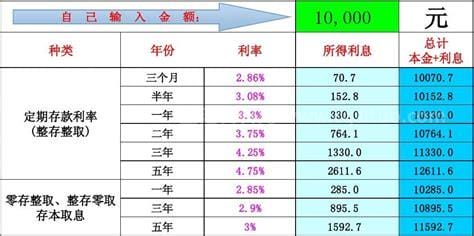
生活中的许多朋友最近问小编利息计算器计算公式的问题,那么小编收集整合后,今天为大家分享关于的相关文章,一起来了解一下吧!本文讲的是利息计算器的在线查询和利息计算器计算公式的对应知识点。希望对你有帮助,也别忘了收
2023-12-16 22:50:01