生活中很多朋友不懂得为什么正多面体只有5种,这个问题小编觉得还是比较简单的,亲自了解了一下这个问题后,就给大家带来了这篇文章,目的当然是能够帮助大家,具体来看下。 1.证明:设正多面体的每个面都是正n边行,每个顶点都是
2023-09-19 00:09:01
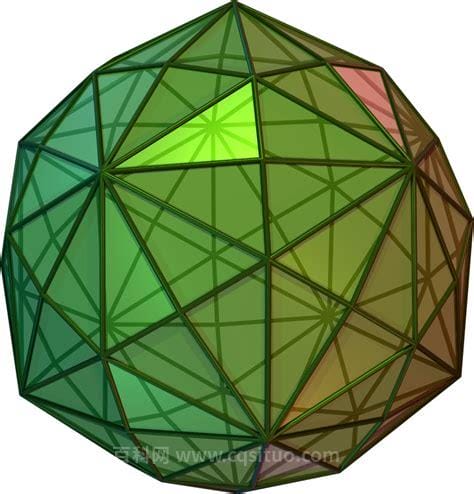
多面体是由四个或更多多边形包围的立体。它有三个相关的定义。在传统意义上,它是三维多面体,而在更新的意义上,它是任意维多面体的有界或无界推广。将后者进一步推广,可以得到一个拓扑多面体。
由几个平面多边形围成的几何称为多面体,由多面体围成的多边形称为多面体面。两个面的公共边称为多面体的边,几个边的公共顶点称为多面体的顶点。如果一个多面体的任意一个面被拉伸,如果所有其他的面都在这个平面的同一边,则称这个多面体为凸多面体。一个多面体至少有四个面,根据面的数量,多面体被称为四面体、五面体、六面体等等。
这是关于多面体的面数、顶点数和棱数的欧拉定理。面是全等正多边形的多面体称为正多面体。面是正三角形的正多面体包括正四面体、正八面体和正二十面体。面为正方形的多面体只有正六面体或正方体,正五边形只有正十二面体。根据欧拉定理,正多面体只有五种。
标签: 多面体
相关文章
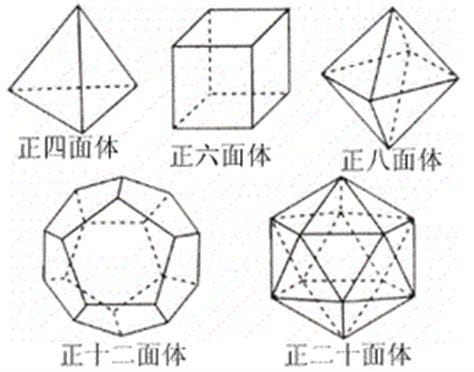
生活中很多朋友不懂得为什么正多面体只有5种,这个问题小编觉得还是比较简单的,亲自了解了一下这个问题后,就给大家带来了这篇文章,目的当然是能够帮助大家,具体来看下。 1.证明:设正多面体的每个面都是正n边行,每个顶点都是
2023-09-19 00:09:01