生活中,有许多的朋友最近问小编wps文字怎么相乘求和的问题,那么小编收集整合后,今天为大家分享关于的相关文章,一起来了解一下吧!【div】【/div】WPS单词如何求和?1.打开一个带有表格数据的WPS文档,用鼠标单击需要输入sum值
2024-03-15 09:18:02

递增数列的求和公式
Sn=n*a1+n (n-1)d/2
对于一个数列,如果从数列的第二项开始,每一项的值不小于前一项的值,则称为递增数列。
递增序列与严格递增序列的区别
严格递增数列模仿严格单调递增函数的定义来增加数列,而递增数列的定义则认为相邻两项相等。
通用术语公式
An=A1+(n-1)d
An=Am+(n-m)d
等差数列前n项的和
Sn=[n(A1+An)]/2
Sn=nA1+[n(n-1)d]/2
等差数列求和公式:等差数列求和=(首数+尾数)*项数/2;
项的公式:等差数列的项= [(尾数-首数)/容差]+1。
数列求和的常用公式
1)1+2+3+.+n=n(n+1)÷2
2)1^2+2^2+3^2+.+n^2=n(n+1)(2n+1)÷6
3) 1^3+2^3+3^3+.+n^3=( 1+2+3+。+n)^2
=n^2*(n+1)^2÷4
4) 1*2+2*3+3*4+.+n(n+1)
=n(n+1)(n+2)÷3
5) 1*2*3+2*3*4+3*4*5+.+n(n+1)(n+2)
=n(n+1)(n+2)(n+3)÷4
6) 1+3+6+10+15+.
=1+(1+2)+(1+2+3)+(1+2+3+4)+.+(1+2+3+...+n)
=[1*2+2*3+3*4+.+n(n+1)]/2=n(n+1)(n+2) ÷6
7)1+2+4+7+11+.
=1+(1+1)+(1+1+2)+(1+1+2+3)+.+(1+1+2+3+...+n)
=(n+1)*1+[1*2+2*3+3*4+。+n(n+1)]/2
=(n+1)+n(n+1)(n+2) ÷6
8)1/2+1/2*3+1/3*4+.+1/n(n+1)
= 1-1/(n+1)= n(n+1)
9)1/(1+2)+1/(1+2+3)+1/(1+2+3+4)+.+1/1+2+3+...+n)
=2/2*3+2/3*4+2/4*5+.+2/n(n+1)
=(n-1) ÷(n+1)
10)1/1*2+2/2*3+3/2*3*4+.+(n-1)/2*3*4*...*n
=(2*3*4*...*n- 1)/2*3*4*...*n
11)1^2+3^2+5^2+.(2n-1)^2=n(4n^2-1)3
12)1^3+3^3+5^3+.(2n-1)^3=n^2(2n^2-1)
13)1^4+2^4+3^4+.+n^4
=n(n+1)(2n+1)(3n^2+3n-1)30
14)1^5+2^5+3^5+.+n^5
=n^2(n+1)^2(2n^2+2n-1)12
15)1+2+2^2+2^3+.+2^n=2^(n+1)–1
公式法
等差数列求和公式:Sn=n(a1+an)/2=na1+n(n-1)d/2等差数列求和公式:Sn = na1(q = 1)Sn = a1(1-q n)/(1-q)=(a1-an×q)/。
位错减法
适用题型:适用于通项公式为等比例等差线性函数相乘的数列形式{an}和{bn},分别为等差数列和等比数列。Sn = A1B1+A2B+A3B3+...+AnBN例如,an = A1+(n-1) DBN = A1 q (n-1)。Cn=anbn Tn=a1b1+a2b2+a3b3+a4b4。+anbn qTn= a1b2+a2b3+a3b4+...+a(n-1)bn+anb(n+1)Tn-qTn = a1 B1+B2(a2-a1)+B3(a3-a2)+...bn[an-a(n-1)]-anb(n+1)Tn(1-q)= a1 B1-anb(n+1)+d(B2+B3+B4+...bn)= a1 B1-an B1 q n+d B2[1-q(n-1)]/(1-q)TN =上式/(1-q)
反向加法
这是用来推导等差数列前n项求和公式的方法,就是把一个数列逆序排列(逆序),然后加到原数列上,就可以得到n (a1+an) sn = a1+a2+a3+。+an sn = an+a (n-1)+a (n-3)。+a1是上下相加。
相关文章
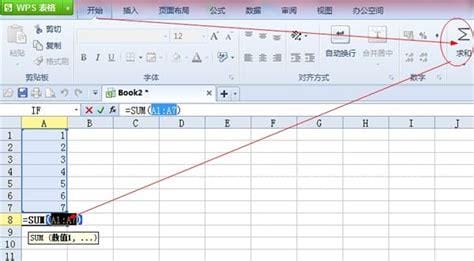
生活中,有许多的朋友最近问小编wps文字怎么相乘求和的问题,那么小编收集整合后,今天为大家分享关于的相关文章,一起来了解一下吧!【div】【/div】WPS单词如何求和?1.打开一个带有表格数据的WPS文档,用鼠标单击需要输入sum值
2024-03-15 09:18:02
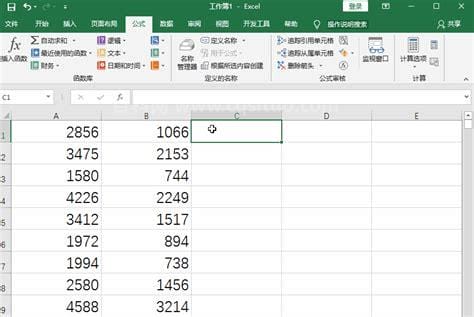
生活的过程中,小伙伴们是不是经常遇到一些很困惑的问题,比如我们今天要说的excel减法函数公式是什么这个问题,要解决这样的问题其实很简单,下面可以跟着小编来具体了解一下吧。在excel中,减法的作用是:IMSUB函数。公式是:A
2024-03-14 22:42:02
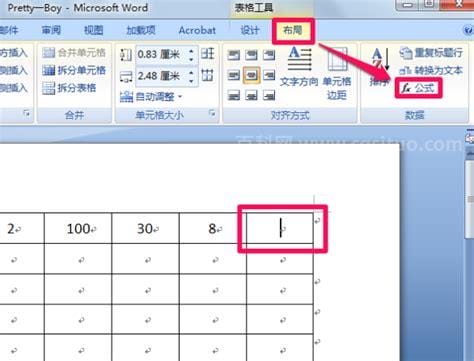
生活中的许多朋友最近问小编word文档里如何求和的问题,那么小编收集整合后,今天为大家分享关于的相关文章,一起来了解一下吧!【div】【/div】word文档中的求和运算方法如下:1.首先,用word打开文档,找到要求和的表格。2.将光
2024-03-14 13:12:03
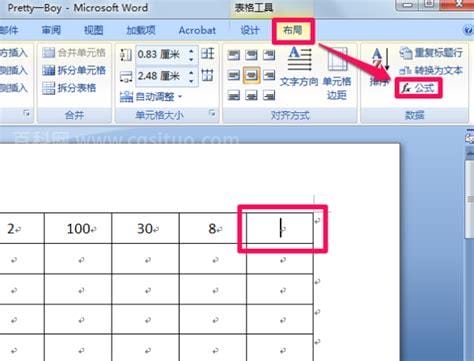
最近很多朋友都遇到了word里面怎么求和公式的问题,今天小编就来为大家解答,快来看看吧。【div】【/div】word文档中的求和运算方法如下:1.首先,用word打开文档,找到要求和的表格。2.将光标放在sum值所在的单元格中,然后单
2024-03-14 11:06:01
有许多朋友最近问小编word里插入公式显示不全的问题,那么小编收集整合后,今天为大家分享关于的解答,一起来了解一下吧!首先,选择无法在word2010中完整显示的公式,如图所示。然后选择开始选项卡并单击段落右下角的45度箭头,如
2024-03-11 22:18:02