生活的过程中,小伙伴们是不是经常遇到一些很困惑的问题,比如我们今天要说的excel减法函数公式是什么这个问题,要解决这样的问题其实很简单,下面可以跟着小编来具体了解一下吧。在excel中,减法的作用是:IMSUB函数。公式是:A
2024-03-14 22:42:02

点到点的距离公式
|AB|=√[(x1-x2) +(y1-y2) ]
两点间距离公式常用于求函数图中两点间的距离和点的坐标,是距离公式之一。两点之间的距离公式描述了点与点之间的关系以及点与点之间的距离。
假设P点(x,y)到直线L的距离:ax+by+c = 0是P点到直线L的垂线的长度,P点到直线的垂线是l & # 39,竖脚为q,则l & # 39B/A的斜率为l & # 39的解析式为y-y = (b/a) (x-x)。把l和l & # 39同时l和l & # 39交点Q的坐标为((b 2x-aby-ac)/(a 2+b 2),(a 2y-abx-bc)/(a 2+b 2))。
pq^2=[(b^2x₀-aby₀-ac)/(a^2+b^2)-x0]^2
+[(a^2y₀-abx₀-bc)/(a^2+b^2)-y0]^2
=[(-a^2x₀-aby₀-ac)/(a^2+b^2)]^2
+[(-abx₀-b^2y₀-bc)/(a^2+b^2)]^2
=[A(-By₀-C-Ax₀)/(A^2+B^2)]^2
+[B(-Ax₀-C-By₀)/(A^2+B^2)]^2
=(a^2+b^2)(ax₀+by₀+c)^2/(a^2+b^2)^2
=(Ax₀+By₀+C)^2/(A^2+B^2)
所以pq = | ax+by+c |/√ (a 2+b 2),公式得到证明。
两点间距离的公式是什么?
两点间距离公式常用于求函数图中两点间的距离和点的坐标,是距离公式的一种。两点之间的距离公式描述了点与点之间的关系以及点与点之间的距离。
两点的坐标是(x1,y1)和(x2,y2),那么两点之间的距离是d=√[(x1-x2)2+(y1-y2)2]。
注意特殊情况
当x1=x2时,两点间的距离为ly1-y2;当y1=y2时,两点间的距离为|x1-x2】。
当然,不考虑特例,所有的公式都被替换,结果都是正确的,但是不必要的时候不要增加自己的计算量。
空间两点间的距离公式
在空间笛卡尔坐标系中,点P(x1,y1,z1)与点Q(x2,y2,z2)之间的距离公式:
d = √( x2-x1)2+(y2-y1)2+(z2-Z1)2;
演绎过程
空间中任意两点A (X1,Y1,Z1)和P (X2,Y2,Z2)都是长方体,使得A和P是它们对角线的顶点。
已知的
C(x2,y1,z1),B(x2,y2,z1)|AP|2=AC|2+|CB]2+|BP|2
APL = √( x2-x1)2+(y2-y1)2+(z2-Z1)2是空间两点间的距离公式。
点到直线的距离公式
设直线L的方程为Ax+By+C=0,点P的坐标为(x0,y0),那么点P到直线L的距离。
就是|AXO+BYO+C|/√A2+B2。逐点公式:当已知直线上的一个点(x0,y0)和方向向量(u,v)时,可以使用,(X-x0)/u=(y-yO)/v(u≠0,v≠0)。
点到直线的距离,即该点到目标直线垂直线的距离。一般公式为:设直线L的方程为Ax+By+C=0,点P的坐标为(x0,y0),则点P到直线L的距离为| axon+byo+ci/√ A2+B2。考虑点(xO,y0,z0)和空间直线x-x1/l=y-y1/m=z-z1/n,其中d =) (X1-x0,Y1-Y0,Z1-Z0) ×(,m,n) |/√ (/2+m2+)
逐点公式:当已知直线上的一个点(xO,yO)和方向向量(u,v)时,可以使用,(x-x0)/u=(y-yo)/v(u=0,v=0)。例如:2x-3y+4=O,2(x+2)=3y,& # 39;。(x+2)/3=y/2,用于求。
相关文章
生活的过程中,小伙伴们是不是经常遇到一些很困惑的问题,比如我们今天要说的excel减法函数公式是什么这个问题,要解决这样的问题其实很简单,下面可以跟着小编来具体了解一下吧。在excel中,减法的作用是:IMSUB函数。公式是:A
2024-03-14 22:42:02
最近很多朋友都遇到了word里面怎么求和公式的问题,今天小编就来为大家解答,快来看看吧。【div】【/div】word文档中的求和运算方法如下:1.首先,用word打开文档,找到要求和的表格。2.将光标放在sum值所在的单元格中,然后单
2024-03-14 11:06:01
有许多朋友最近问小编word里插入公式显示不全的问题,那么小编收集整合后,今天为大家分享关于的解答,一起来了解一下吧!首先,选择无法在word2010中完整显示的公式,如图所示。然后选择开始选项卡并单击段落右下角的45度箭头,如
2024-03-11 22:18:02
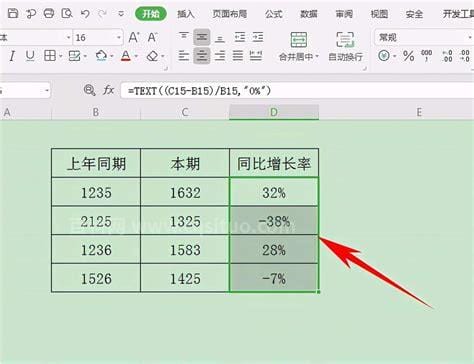
大家在生活的过程中总会遇到一些问题,比如同比的计算公式,那么今天小编就为大家分享关于的相关文章,希望在这篇文章中你能了解到相关内容。计算公式:同比增长率=(期数-期数)÷期数×100%。某个指标的同比增长率=(当前某个
2024-03-10 04:24:01
excel函数if公式怎么用?希望不清楚的大家在这看一看,小编已经为大家把这个问题总结好了,希望接下来的能帮大家解决这个问题,看完了记得分享哦!边肖通过一个简单的例子告诉你如何使用if公式!假设数据在A1输入,在B1判断。如果
2024-03-10 03:42:02