有些小伙伴经常会碰到准确率100的生男生女公式的问题,但是对于不是非常了解,给小伙伴带来了很多困惑,但小伙伴们找到这里算是没白来,因为小编就带大家详细讲解一下,具体内容如下。很多孕妇特别想知道胎儿的性别,以便给孩子
2023-11-20 10:48:01
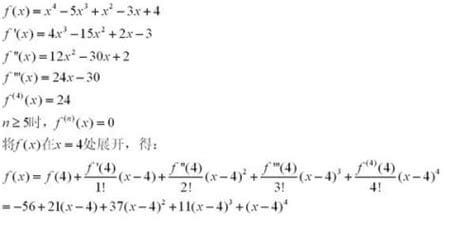
比如说。
函数f(x)=3x+4是多项式函数(线性函数),an=3n+4是多项式序列,但实际上是等差数列。
所以我们有了第一个明显的结论:等差数列是多项式级数。
当然多项式级数的范围比等差数列大。
类似于等差数列,我们也可以考虑多项式数列的容差。
设线性多项式序列an=3n+1,则容差为常数3。
神说:猜测数学远比证明数学重要。所以我猜到了第二个结论:
n次多项式序列的前后项之差是n-1次多项式序列。
(第一项和第二项是我很开心的表情,标准描述应该是:每一项和前一项的区别)
如何求多项式数列前n项之和?
我们发现多项式序列
所以,我们求和的时候,可以逐项求和。
学生能背的公式有:(老师逼的)
高等级的;级别较高的;较重要的...考试的时候我选择了放弃!
得了吧,到了这里让你选择放弃是我的错。
如果你不读下去,你绝对是看不起我。你以为我写不出你看得懂的数学吗?
让我们看看
怎么算,然后把方法用同样的方法。
我们发现这个计算过程其实用的是高阶(n+1)展开,然后可以叠加。
同样的,我们可以计算
然后代入已知公式,化简!
反过来,高阶计算,虽然计算繁琐,但确实可以计算出我们需要的任何求和公式。
正是因为这个计算复杂,所以我们在高考中只敢要求最多两次。(就算演绎不出来也能背下来吧?)
竞争也喜欢玩这个,当然不会仅限于第二次。
你为什么喜欢考试和比赛?因为这个解法看起来很帅,用的是二项式定理和叠加法,消除很多人需要大量的计算。
但是,氮气,我是极度不喜欢这种溶液的!因为这种解决方法除了能在考试中打败考生之外一无是处。
我有一个更漂亮简洁的算法。
表演时间到了。
我们已经知道,如果f(x)是n次多项式,那么f(x+1)-f(x)是n-1次多项式(见前面的结论2)。
搞定了。问题可以转化为一次高的多项式函数,方程就可以解了,计算量少得多。
不是好多了吗?用解方程代替复杂的求和符号是划算的。
不要急着“再看”。哦,我有一个更漂亮更简洁的解决方案。
我们发现多项式级数an的前n项之和也是多项式级数,只是次数高了一倍,所以可以直接用待定系数法求!
简单粗暴,直截了当,不就是《孤中九剑》吗!
什么?你觉得这个方程很难解,计算只是比上一个解多了很多。
好吧,我输了。
相关文章

有些小伙伴经常会碰到准确率100的生男生女公式的问题,但是对于不是非常了解,给小伙伴带来了很多困惑,但小伙伴们找到这里算是没白来,因为小编就带大家详细讲解一下,具体内容如下。很多孕妇特别想知道胎儿的性别,以便给孩子
2023-11-20 10:48:01

生活中有许多朋友问小编准确率100的生男生女公式,那么今天小编就为大家解决一下这个问题,希望对你有所帮助。很多准妈妈都很好奇自己肚子里胎儿的性别,但是医生又说不出胎儿的性别,所以只能在网上寻找鉴定胎儿性别的方法
2023-11-19 21:48:01

大家好,kj和卡路里换算公式小编来为大家解答。呢,很多朋友还不理解,现在让我们一起来介绍下,希望能帮助到你!卡路里是一个能量单位,它被定义为在1个大气压下将1克水升高1摄氏度所需的热量。卡路里在营养测量和健身手册中被
2023-11-19 02:09:01

有许多的朋友最近问小编男人能熬多久不碰女人的问题,那么小编收集整合后,今天为大家分享关于的相关文章,一起来了解一下吧!通常男人可以七天不碰女人。一旦超过7天不碰女人,就会有一种冲动,出现频繁射精,性欲增强,遗精,忍不住
2023-11-10 18:48:01
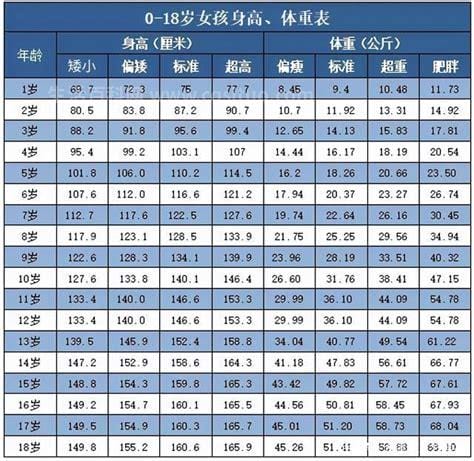
大家在生活的过程中总会遇到一些问题,比如1一18岁身高体重标准表范围计算公式2023优质,那么今天小编就为大家分享关于的相关文章,希望在这篇文章中你能了解到相关知识。孩子的健康成长是家长们头疼的问题。许多家庭每年
2023-11-10 16:27:01