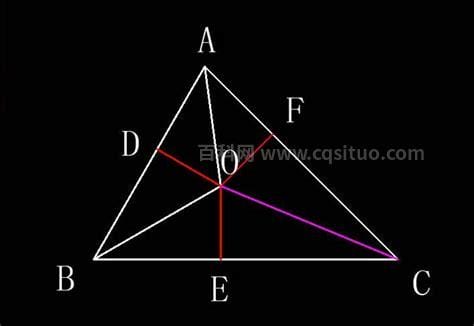
三角形重心(三角形重心性质)

文化常识 2023-09-25 20:59:22

大家在中遇到的三角形重心(三角形重心性质)这样的问题有没有答案呢?答案是肯定的，对于大部分朋友来说解决这样的问题还是非常重要的，所以小编给大家做了个整理，一起来看下面的内容。

三角形重心(三角形重心性质)

1.重心到顶点的距离与重心到对面中点的距离之比为2: 1。

2.重心和三角形的三个顶点组成的三个三角形的面积相等。

3.从重心到三角形三个顶点的距离的平方和最小。

证明方法:

设三角形的三个顶点为(x1，y1)，(x2，y2)，(x3，y3)平面上的任一点为(x，y)，则该点到三个顶点的距离的平方和为:

(x1-x)2+(y1-y)2+(x2-x)2+(y2-y)2+(x3-x)2+(y3-y)2

= 3 x2-2x(x1+x2+x3)+3 y2-2y(y1+y2+y3)+x12+x22+x32+y12+y22+y32

= 3[x-1/3 *(x1+x2+x3)]2+3[y-1/3 *(y1+y2+y3)]2+x12+x22+x32+y12+y22+y32-1/3(x1+x2+x3)2-1/3(y1+y2+y3)2

显然，当x = (x1+x2+x3)/3，y = (y1+y2+y3)/3(重心坐标)时，

上面的公式得出了最小值X12+X22+X32+Y12+Y22+Y32-1/3(X1+X2+X3)2-1/3(Y1+Y2+Y3)2。

最后得出结论。

4.在平面直角坐标系中，重心的坐标是顶点坐标的算术平均值。

5.三角形到三条边的距离的乘积最大的点就是重心。

需要多项式不等式的柯西证明！

6.在△ABC中，如果MA向量+MB向量+MC向量=0(向量)，那么点M就是△ABC的重心，反之亦然。

7.设△ABC的重心为g点，平面上有一点O，则向量OG=1/3(向量OA+向量OB+向量OC)。