最近很多朋友都遇到了解密入门级饮品,什么叫口粮茶的问题,今天小编就来为大家解答,快来看看吧。1、什么叫口粮茶1.配给茶是指性价比高,可以日常饮用的茶叶。说白了就是便宜点的好茶。主要思路是便宜实惠,日常饮用。2.价格
2024-01-09 06:54:01
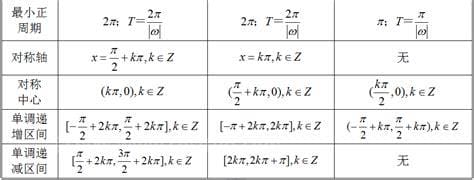
函数入门基础知识
函数入门基础知识,三角函数的公式看似很多很复杂,但其实只要掌握了三角函数的内在规律和本质,是学好三角函数的关键,你会发现三角函数的公式之间有很强的联系。下面分享函数入门基础知识。
三角函数的公式怎么记?
1.“即使奇变,符号也会看象限”:
“奇、偶”是指π/2的倍数的奇偶性,“变与不变”是指一个三角函数名称的变化;“变”是指正弦变余弦,正切变余切。(反之亦然)“符号看象限”的含义是:以角α为锐角,不考虑角α所在的象限,看象限角N (π/2) α是什么,从而得出方程的右边是正还是负。
2、符号判断公式:
“一个是好的;两个正弦;三条切线;四余弦”。这个12字公式的含义是:第一象限任意角度的四个三角函数为“+”;只有第二象限的正弦是“+”,其余都是“-”;第三象限只有切线和余切是“+”,其余都是“-”;第四象限只有余弦是“+”,其他都是“-”。
“ASCT”与Z相反,表示“all”、“sin”、“cos”、“tan”是正三角函数,对应于字母Z反过来所占的象限。
3.三角函数的本质
三角函数是数学中初等函数中属于超越函数的一类函数。它们的本质是任意角的集合和一组比值的变量之间的映射。通常的三角函数是在平面直角坐标系中定义的,其定义域是整个实数域。另一个定义在直角三角形里,但不完整。现代数学把它们描述为无穷数列的极限和微分方程的解,并把它们的定义扩展到复数系统。
它包含六个基本功能:正弦,余弦,正切,余切,割线和余切。由于三角函数的周期性,它不具有单值函数意义上的反函数。三角函数在复数中有重要的应用。三角函数也是物理学中的常用工具。
1.初中数学函数的知识怎么学?
熟悉坐标系
一年级函数学完坐标轴,二年级开始学坐标系。坐标系是所有函数的容器,需要在所有函数中体现出来。
学会表达观点
另外,你需要学会用初中函数表示点,学会用横坐标和纵坐标表示点的位置和特征。学会表达点的位置、运动和特征。
理解函数的概念
理解自变量和因变量的概念,进而理解函数的概念。只有理解了函数的概念,才能进行初中函数题的计算。
我们应该充分利用抛物线“顶点”的作用
准确灵活地找到“顶点”,形式为y=a(x+h)2+K→顶点(-h,K)。对于其他形式的二次函数,我们可以把它变成顶点来求顶点。
用顶点画一个草图。大多数情况下,我们只需要画一个草图就可以帮助我们分析和解决问题。这时候我们可以根据抛物线的顶点和开口的方向画出抛物线的大概图像。
2.初中函数的基本概念。
线性函数也是线性函数,可以用x,y坐标轴上的直线来表示。当一个线性函数中一个变量的值确定后,另一个变量的值可以由一个线性方程确定。
函数的基本概念:在一个变化的过程中,有两个变量X和Y,对于X的每一个确定值,在Y中都有一个唯一的确定值与之对应,那么我们就说Y是X的函数,或者说X是自变量,Y是因变量。
表示为y=kx+b(k≠0,k和b为常数)。当b=0时,称y是x的正比函数,正比函数是线性函数中的特例。可以表示为y=kx。
初中函数入门基础知识如下:
一.定义
函数的定义:一般来说,在一个变化的过程中,如果有两个变量X和Y,并且对于X的每一个确定值,Y都有唯一的确定值与之对应,那么我们说X是自变量,Y是X的函数,Y的值称为函数值。
第二,分类
(1)常数函数:当X取定义域中的任意数时,有y=C(C为常数),则函数y=C称为常数函数,其像是平行于X轴的直线或直线的一部分。
(2)、线性函数:一般形式为y=kx+b(k,b为常数,k≠0),其中x为自变量,y为因变量。特别是当b=0时,y=kx+b(k为常数,k≠0),y称为x的正比函数。
第三,函数的表示
(1)解析方法:两个变量之间的关系有时可以用包含这两个变量和数学运算符号的方程来表示,称为解析方法。
(2)列表法:列出自变量X的一系列值和函数Y的相应值来表示函数关系。这种表示方法称为列表法。
(3)形象法:用形象表示函数关系的方法称为形象法。
四、线性函数的图像和性质
(1)线性函数上的任意点P(x,y)满足方程:y = kx+b。
(2)线性函数与Y轴的交点坐标始终为(0,b),与X轴的交点坐标始终为(-b/k,0)。
(2)比例函数的像总是穿过原点。
五、二次函数的三种表达式
(1)通式:y = ax ^ 2+bx+c(a,b,c为常数,a≠0)。
(2)顶点类型:y = a (x-h) 2+k。
(3)交点:y = A(x-X)(X-X)[仅适用于与X轴有交点A(X,0)和B(x,0)的抛物线]。
二次函数图像的对称关系
对于通式:
①Y = ax2+bx+c和y=ax2-bx+c两幅图像关于Y轴对称。
②两幅图像y=ax2+bx+c和y=-ax2-bx-c关于X轴对称。
③ y=ax2+bx+c和y=-ax2-bx+c-b2/2a关于顶点对称。
④ y=ax2+bx+c和y=-ax2+bx-c关于原点中心对称。
相关文章

最近很多朋友都遇到了解密入门级饮品,什么叫口粮茶的问题,今天小编就来为大家解答,快来看看吧。1、什么叫口粮茶1.配给茶是指性价比高,可以日常饮用的茶叶。说白了就是便宜点的好茶。主要思路是便宜实惠,日常饮用。2.价格
2024-01-09 06:54:01
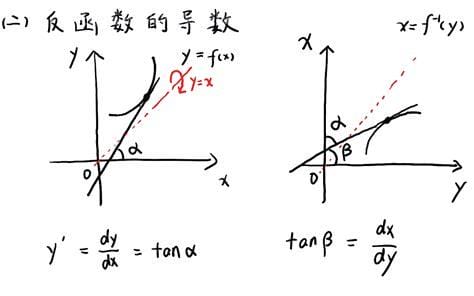
最近很多朋友都遇到了如何反函数求导的问题,今天小编就来为大家解答,快来看看吧。求反函数的9种方法 只有一种方法可以找到反函数。就是反解方程,交换xy位置,求定义域。要找到反函数:1.利用反解方程,把X看成一个未知数,把Y
2024-01-07 16:24:01

生活中很多朋友不懂得青骄第二课堂2020期末答案大全,这个问题小编觉得还是比较简单的,亲自了解了一下这个问题后,就给大家带来了这篇文章,目的当然是能够帮助大家,具体来看下。青教第二课堂2020知识答案大全。青教第二课堂
2024-01-07 08:18:01

生活中有许多朋友问小编国家禁毒的基本之策是什么,那么今天小编就为大家解决一下这个问题,希望对你有所帮助。我国禁毒的基本知识治本之策是什么 中国禁毒的根本出路在于禁毒宣传教育。根据《中华人民共和国禁毒法》的
2024-01-07 07:54:01

一国两制的前提和基础是什么是各位朋友所需要解决的问题,问题理解之后可以给朋友带来很大的帮助,所以今天小编就给大家带来的详细讲解,一起来看看吧。一国两制的前提和基础是什么 1.一国两制原则的前提是:一个中国,即中华
2024-01-06 17:48:01