对数正态分布(对数正态分布期望推导)

大家在生活的过程中总会遇到一些问题，比如对数正态分布(对数正态分布期望推导),那么今天小编就为大家分享关于的相关文章，希望在这篇文章中你能了解到相关内容。

对数正态分布(对数正态分布期望推导)

点击上方关注，尽在AI中国

概率分布就像3D眼镜。它们使熟练的数据科学家能够识别完全随机变量中的模式。

在某种程度上，大多数数据科学或机器学习技能都是基于对数据概率分布的一些假设。

这就使得概率知识成为统计学家构建工具箱的基础。如果你正在思考如何成为一名数据科学家，那么这是第一步。

废话少说，说重点吧！

什么是概率分布？

在概率论和统计学中，随机变量是可以随机取不同值的变量，比如“我看到的下一个人的身高”或者“我下一个拉面碗里厨师的头发数”。

给定一个随机变量x，我们想描述它取哪个值。更重要的是，我们想描述一个变量取某个值x的可能性有多大。

比如X是“我女朋友养了几只猫”，那么这个数字可能是1，甚至是5，10。

当然，一个人不能有一只消极的猫。

所以我们希望用一种清晰的数学方法来表达变量X可以取的每一个可能值，以及事件发生的可能性(X= x)。

为了做到这一点，我们定义了一个函数P，使得P(X = x)是变量X的值为X的概率。

我们也可以用p(x；x)而不是离散值。这一点非常重要。

p是变量的密度函数，代表变量的分布。

随着时间的推移，科学家们意识到，自然界和现实生活中的许多事物往往表现相似，变量共享一个分布或具有相同的密度函数(或相似的函数)。

要使p成为实用的密度函数，需要一些条件。

P(X =x) <= 1 对于任意值X, P(X =x)必须小于等于1P(X =x) >= 0 对于任意值X, P(X =x)必须大于等于0对于任意值X，P(X =x) 所有值的和为1(X取任意值的概率，加起来等于1）

离散和连续随机变量分布

随机变量可分为两组:离散型随机变量和连续型随机变量。

离散随机变量

离散变量有一组离散的可能值，每个值的概率不为零。

例如，当我们掷硬币时，如果我们说

X = \" 1如果硬币是正面，0如果是反面\ "

P(X = 1) = P(X = 0) = 0.5

然而，请注意，离散集合不一定是有限的。

几何分布，一个事件的概率为p，第一次成功的概率是测试k次后得到的:

k可以取任何非负正整数。

请注意，所有可能值的概率之和仍然是1。

连续随机变量

如果

X = "从我的头上随机拔下的一根头发的长度，以毫米为单位(不四舍五入)"

x可以取什么值？我们知道负数在这里没有意义。

但是，如果你说的是1 mm而不是1.1853759之类的，我要么怀疑你的测量技术，要么怀疑你的测量报告是错的。

连续随机变量可以取给定(连续)区间内的任何值。

如果x是连续的随机变量，x的概率分布密度函数用f(x)表示。

使用p (a

为了得到X取任意指定实数A的概率，需要对X从A到b的密度函数进行积分。

既然你知道了什么是概率分布，那我们就来学习一些最常见的分布吧！

一、伯努利概率分布

伯努利分布是最简单的随机变量之一。

它代表一个二元事件:“这件事发生了”vs“这件事没发生”，以p值作为唯一的参数来表示事件发生的概率。

伯努利分布的随机变量b的密度函数为:

P(B = 1) = p，P(B =0)= (1- p)

这里B=1表示事件发生了，B=0表示事件没有发生。

注意这两个概率加起来是1，所以不可能有其他值。

二、均匀概率分布

均匀随机变量有两种:离散随机变量和连续随机变量。

离散均匀分布将取一组(有限)值S，并为每个值分配1/n的概率，其中n是S中元素的数量。

这样，如果变量y在{1，2，3}中是一致的，那么每个值的概率是33%。

骰子是一个非常典型的离散均匀随机变量。典型的骰子有一组值{1，2，3，4，5，6}，元素个数为6，每个值的概率为1/6。

连续均匀分布只取A和B两个值作为参数，在它们之间的区间内给每个值赋予相同的密度。

这意味着Y在一个区间(从C到D)中取值的概率与其相对于整个区间(从B到A)大小的大小成正比。

因此，如果y在a和b之间均匀分布，那么

因此，如果y是1和2之间的均匀随机变量，

p(1 & lt；X & lt2)=1，P(1 & lt；X & lt1.5) = 0.5

Python的random包的random方法采样一个均匀分布在0和1之间的连续变量。

有趣的是，可以证明，给定一个均匀随机值生成器和一些微积分，可以对任何其他分布进行采样。

三、正态概率分布

正态分布变量在自然界中很常见，它们是正态的，这就是这个名字的由来。

如果你把所有同事集合起来，测量他们的身高，或者称体重，然后用结果画一个直方图，结果很可能接近正态分布。

如果你取任意一个随机变量的样本，对这些测量值取平均值，多次重复这个过程，平均值也会有一个正态分布。这个事实非常重要。它被称为统计学的基本定理。

正态分布变量:

呈对称钟形曲线, 以均值为中心（通常称为μ）。可以取实空间上的所有值，正态曲线由均数所在处开始，分别向左右两侧逐渐均匀下降。标准差σ决定了分布的幅度。几乎无处不在

在大多数情况下，如果你测量任何经验数据，它是对称的，你一般可以假设它是正态分布的。

比如掷出k个骰子，然后把结果加起来，你会得到一个正态分布。

四、对数正态分布概率分布

对数正态概率分布是一种罕见的正态概率分布。

如果变量Y = log(X)服从正态分布，则变量X称为对数正态分布。

在直方图中，对数正态分布是不对称的，标准差σ越大，分布越不对称。

我觉得对数正态分布值得一提，因为大多数基于货币的变量都是这样的。

例如，如果你观察任何与金钱相关的变量的概率分布

某银行最近一次转账的金额。华尔街最新成交量。公司特定季度收益。

它们通常不是正态概率分布，而是更接近对数正态随机变量。

如果你能想到你在工作中遇到的任何其他对数正态变量，请在评论中发表你的看法！尤其是金融以外的东西)。

五、指数概率分布

指数概率分布也随处可见，这与泊松分布概率的概念密切相关。

泊松分布直接抄袭* * *，是“一个事件以恒定的平均速率连续独立发生的过程”。

这意味着如果:

你有很多事情要做。它们以一定的速度发生(不随时间改变)。任何一个成功的事件都不应该影响另一个成功的事件。

泊松分布可能是发送到服务器的请求、超市中的交易或湖中钓鱼的鸟。

想象一个频率为λ的泊松分布(例如，事件每秒发生一次)。

指数随机变量模拟一个事件发生后下一个事件发生所需的时间。

有趣的是，在泊松分布中，事件可以发生在0到∞之间的任何时间区间(概率递减)。

这意味着无论你等多久，事件发生的可能性都不是零。这也意味着短时间内可能会发生多次。

在课堂上，我们经常开玩笑说公交车的到站是泊松分布。我觉得你给某些人发WhatsApp消息时的响应时间也符合这个标准。

λ参数调整活动的频率。它将事件实际发生所需的预期时间集中在某个值上。

这意味着，如果我们知道每15分钟就有一辆出租车经过我们的街区，即使理论上我们可以永远等下去，我们也很可能等不到30分钟。

数据科学中的指数概率分布

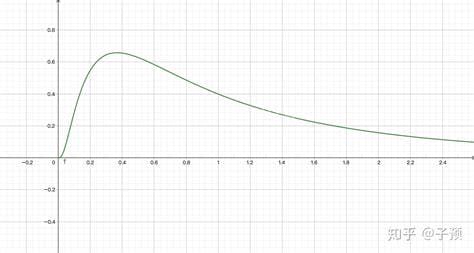
这是指数分布随机变量的密度函数:

假设您有一个变量样本，并想看看它是否可以用指数分布的变量来建模。

更好λ参数可以容易地估计为采样值平均值的倒数。

指数变量非常适合建模任何罕见但巨大的异常值。

这是因为它们可以取任何非负值，但频率会随着值的增大而减小。

特别是在极重的样本中，您可能希望估计λ中值而不是平均值，因为中值对异常值更稳健。在这一点上，你的兴趣可能不同，所以你对此有所保留

结论

总之，作为一名数据科学家，我认为学习基础知识非常重要。

概率统计可能没有深度学习或者无监督机器学习那么华而不实，但是它们是数据科学和机器学习的基石。

根据我的经验，在不知道它们遵循哪种分布的情况下，提供有特征的机器学习模型是一个糟糕的选择。

记住指数分布和正态分布的普遍性，以及罕见的对数正态分布也是很好的。

当训练机器学习模型时，了解它们的特征、用途和性能将会扭转这种模式。在进行任何类型的数据分析时，记住它们通常是有益的！