生活的过程中,小伙伴们是不是经常遇到一些很困惑的问题,比如我们今天要说的excel减法函数公式是什么这个问题,要解决这样的问题其实很简单,下面可以跟着小编来具体了解一下吧。在excel中,减法的作用是:IMSUB函数。公式是:A
2024-03-14 22:42:02
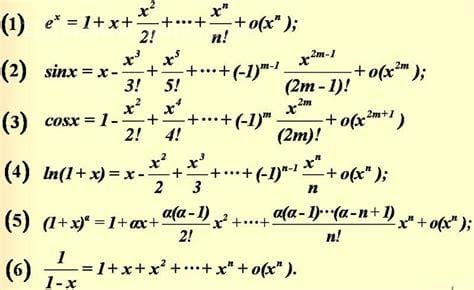
泰勒展开式常用公式e^x=lim(1+x/n)^n。
1.泰勒公式是利用函数在某一点的信息来描述其附近值的公式。来自微积分的泰勒定理,如果函数足够光滑,泰勒公式就可以在已知函数各阶导数值的情况下,以这些导数值为系数构造一个多项式来逼近函数在这一点的邻域内的值。
2.泰勒公式是用一个关于(x-x0)的n次多项式来逼近一个在x=x0处有n阶导数的函数f(x)的方法。
3.泰勒公式虽然形式上并不复杂,但其路线却比较奇怪。几乎所有的教材都直接给出这个公式,然后证明相应的结论。泰勒级数是用无穷项相加来表示函数,也就是级数,这些相加的项是由函数在某一点的导数得到的。
在数学中,泰勒公式是用函数在某一点的信息来描述其附近的值的公式。如果函数足够光滑,在已知函数各阶导数值的情况下,泰勒公式可以用这些导数值作为系数,构造一个多项式来逼近该点邻域内的函数值。泰勒公式也给出了这个多项式与实际函数值的偏差。
泰勒公式得名于英国数学家布鲁克·泰勒。他在1712年的一封信中首次描述了这个公式,尽管詹姆斯·格雷·高里在1671年发现了它的一个特例。1797年以前,拉格朗日首先提出了现在形式的带余项的泰勒定理。
希腊哲学家芝诺在考虑用无穷级数求和得到有限结果的问题时,得出了一个不可能的结论——芝诺悖论。最著名的两个悖论是“阿喀琉斯追乌龟”和“箭不动”。
后来亚里士多德在哲学上批驳了芝诺悖论,数学的这一部分直到德谟克利特和后来的阿基米德才得以解决。阿基米德用穷举法把一个无穷级数逐步细分,得到的结果有限。
14世纪马达瓦发现了一些特殊的函数,包括正弦、余弦、正切、反正切等三角函数的泰勒级数。
在17世纪,詹姆斯·格雷果利也继续了这一领域的研究,并出版了几部麦克劳林丛书。直到1712年,英国牛顿学派最杰出的代表之一的数学家泰勒提出了一个普遍的方法,这就是泰勒级数。爱丁堡大学的科林·麦克劳林教授发现了泰勒级数的一个特例,叫做麦克劳林级数。
标签: 公式
相关文章
生活的过程中,小伙伴们是不是经常遇到一些很困惑的问题,比如我们今天要说的excel减法函数公式是什么这个问题,要解决这样的问题其实很简单,下面可以跟着小编来具体了解一下吧。在excel中,减法的作用是:IMSUB函数。公式是:A
2024-03-14 22:42:02
最近很多朋友都遇到了word里面怎么求和公式的问题,今天小编就来为大家解答,快来看看吧。【div】【/div】word文档中的求和运算方法如下:1.首先,用word打开文档,找到要求和的表格。2.将光标放在sum值所在的单元格中,然后单
2024-03-14 11:06:01
有许多朋友最近问小编word里插入公式显示不全的问题,那么小编收集整合后,今天为大家分享关于的解答,一起来了解一下吧!首先,选择无法在word2010中完整显示的公式,如图所示。然后选择开始选项卡并单击段落右下角的45度箭头,如
2024-03-11 22:18:02
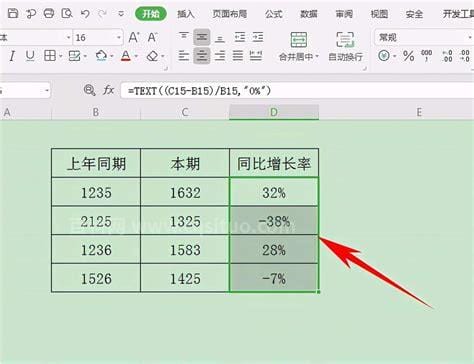
大家在生活的过程中总会遇到一些问题,比如同比的计算公式,那么今天小编就为大家分享关于的相关文章,希望在这篇文章中你能了解到相关内容。计算公式:同比增长率=(期数-期数)÷期数×100%。某个指标的同比增长率=(当前某个
2024-03-10 04:24:01
excel函数if公式怎么用?希望不清楚的大家在这看一看,小编已经为大家把这个问题总结好了,希望接下来的能帮大家解决这个问题,看完了记得分享哦!边肖通过一个简单的例子告诉你如何使用if公式!假设数据在A1输入,在B1判断。如果
2024-03-10 03:42:02