勾股定理是谁发现的

生活中有些小伙伴会遇到勾股定理是谁发现的的问题，没有关系，通过这篇文章就能帮大家轻松解决，跟着小编我们一起来看下文章。

传统上是古希腊的毕达哥拉斯证明的。据说毕达哥拉斯证明了这个定理后，把一百头牛斩首以示庆祝，所以也叫“百牛定理”。

而在中国，《周篇·舒静》记载了勾股定理的一个特例，据传是商代的商高发现的，所以也叫商高定理。三国时期的赵爽在《周髀算经》中对勾股定理做了详细的注释作为证明。法国和比利时叫驴桥定理，埃及叫埃及三角。

勾股定理:在任何直角三角形中，两条直角边的平方和必须等于斜边的平方。

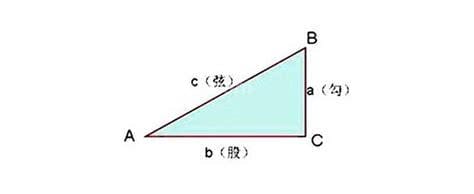
勾股定理是一个基本的几何定理，意思是直角三角形的两个直角的平方和等于斜边的平方。中国古代把直角三角形叫做勾股定理，较小的直角边是钩，另一条较长的直角边是弦，斜边是弦，所以这个定理叫做勾股定理，也有人叫它商高定理。

勾股定理的证明方法大约有500种，勾股定理是数学中被证明最多的定理之一。

勾股定理是人类早期发现并证明的重要数学定理之一。它是用代数思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一。

在中国，商朝的商高提出了勾股定理的一个特例。在西方，公元前6世纪古希腊的毕达哥拉斯学派首先提出并证明了这个定理。他通过推导证明了直角三角形斜边的平方等于两个直角的平方之和。

中国简史

公元前11世纪，数学家商高(生于西周初年)提出了“勾三、顾四、武贤”。成书于公元前一世纪的《周礼》记载了商皋和的一段对话。尚高说:“...所以折矩，勾宽三，股修四，过角五。”含义:当直角三角形的两条直角边分别为3(勾)和4(弦)时，半径角(弦)为5。以后人们会简单地说这个事实是“三股四弦五”，根据这个典故，勾股定理就叫做商高定理。

公元3世纪，三国时期的赵爽在《周易·suan经》中对勾股定理做了详细的注释，该书记载在《九章算术》中。赵爽创建了勾股方图，由数形结合得到，并给出了勾股定理的详细证明。后来刘徽也在刘徽的笔记中证明了勾股定理。

中国清末数学家华·提出了勾股定理的二十多种证明。