许多朋友不知道隐函数的导数怎么求？隐函数求导公式、法则以及方法是什么？怎么办，对此很疑惑，那么今天就和小编一起来看看吧，一定可以帮助到你。第01步：隐函数的求导规律与复合函数的求导规律相同。由xy & sup2-e^xy+2=0,y&s
2023-10-20 19:06:01
ln的运算法则是什么？
生活百科 2023-10-21 05:12:02
许多朋友不知道ln的运算法则是什么？怎么办，对此很疑惑，那么今天就和小编一起来看看吧，一定可以帮助到你。
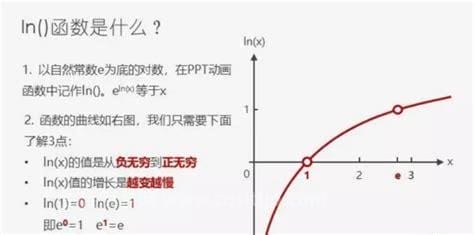
ln函数的算法:ln(MN)=lnM+lnN，ln(M/N)=lnM-lnN，LN (m n) = NLnm，ln1=0，lne=1。注意，反汇编后，在没有LN (m+n) = LNM+的情况下，M和N需要大于0。
一般如果a的幂(a大于0，a不等于1)等于n(n >；0)，那么这个数b叫做n的底数的对数，记为logaN=b，读作n的底数的对数，其中a叫做对数的底数，n叫做实数。一般情况下，函数y=log(a)X，(其中a为常数，a >；0且a不等于1)称为对数函数，它实际上是指数函数的反函数，可以表示为x = a y，因此指数函数中a的规定也适用于对数函数。
算法
ln(MN)=lnM+lnN
ln(M/N)=lnM-lnN
ln(M^n)=nlnM
ln1=0
lne=1
注意，反汇编后，m和n需要大于0。没有ln(M+N)=lnM+lnN，也没有ln(M-N)=lnM-lnN。Lnx是E X的反函数，也就是说当LN (E X) = X时，lnx等于多少，也就是E的多少次方等于X。
函数的定义通常分为传统定义和现代定义。这两种功能定义的本质是一样的，只是叙事概念的出发点不同。传统的定义是从运动变化的角度，现代的定义是从集合和映射的角度。函数最初是由中国清代数学家李在他的《代数》一书中翻译的。他之所以这样翻译，是因为“谁相信这个变量，谁就是那个变量的函数”，即函数意味着一个量随另一个量变化，或者一个量包含另一个量。
标签： 法则
相关文章
- 详细阅读
-
对数函数运算法则是什么？详细阅读
小伙伴们在生活的过程中会遇到很多问题，比如有些小伙伴对对数函数运算法则是什么？不是很懂，不过没有关系，小编今天就给大家详细讲解一下这个问题，具体内容如下。第01步：两个正数的乘积的对数等于这两个基数相同的数的对数之
2023-10-20 00:48:01
-
ln的运算法则及公式详细阅读
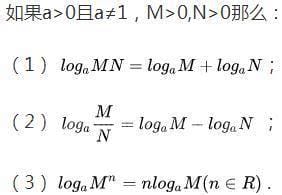
生活中有些小伙伴会遇到ln的运算法则及公式的问题，没有关系，通过这篇文章就能帮大家轻松解决，跟着小编我们一起来看下文章。ln函数的算法:ln(MN)=lnM+lnN，ln(M/N)=lnM-lnN，ln (m n) = nlnm，ln1=0，lne=1。(1)log(1/a)(1/b)=lo
2023-10-13 04:20:01
-
负数的加减乘除运算法则口诀详细阅读
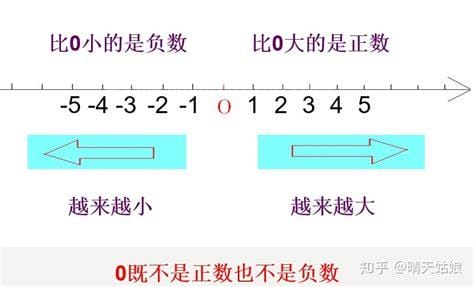
生活中有许多的朋友最近问小编负数的加减乘除运算法则口诀的问题，那么小编收集整合后，今天为大家分享关于的相关文章，一起来了解一下吧！加减乘除公式加减公式:正相加，和为正。负和负相加，和为负。负担减轻了，就是正面的。负
2023-10-12 01:08:01
-
积的乘方法则详细阅读
有许多朋友最近问小编积的乘方法则的问题，那么小编收集整合后，今天为大家分享关于的解答，一起来了解一下吧！乘积相乘，先将乘积中的各个因子分别相乘，再将得到的幂相乘。用字母表示为:(a×b)^n=a^n×b^n这个积的乘方法则也适
2023-10-08 00:21:23