生活中，很多小伙伴不知道古埃及的金字塔是怎样建成的20字?今天小编针对这个问题做了这篇文章，详细内容我们来看一下。金字塔是古埃及人用石头堆起来的，质心靠近底座。古代金字塔大多是用石头堆砌而成，质心靠近底座。等级
2023-10-13 16:53:01
笛卡尔是怎样发现直角坐标系的
生活百科 2023-10-13 18:24:26
大家在生活的过程中总会遇到一些问题，比如笛卡尔是怎样发现直角坐标系的,那么今天小编就为大家分享关于的相关文章，希望在这篇文章中你能了解到相关内容。
坐标系建立于1637年。笛卡尔创立坐标系那一年还有一个故事。笛卡尔年轻时身体并不强壮，经常生病卧床休息。时间长了，他养成了躺在床上思考的习惯。
在研究如何把数和形结合起来，用代数描述几何的时候，笛卡尔参军的时候刚到一个陌生的地方。他辗转反侧，难以入眠，开始思考几何和代数的结合。
但是，我的思路一时半会儿也说不清楚。笛卡尔无聊之时，看到墙上有蜘蛛忙着爬来爬去织网，心中大增。他突然产生了兴趣，仔细观察起来。在观看蜘蛛有规律地交替编织网格时，笛卡尔在冥想中灵机一动:蜘蛛的运动轨迹可以通过这些线来定位吗？蜘蛛的位置是否也可以由直线相交形成的点来确定？
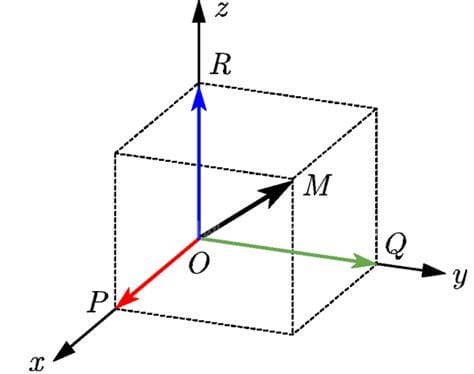
想到这，他立刻从床上爬了起来。他仔细观察了两个垂直的墙壁和天花板的交叉点，三个平面相互垂直。他拿出笔，画了三条垂直的直线，分别代表两堵墙的交点和墙与天花板的交点，又在纸上画了一个点，代表蜘蛛在墙上爬行。从这个点到蜘蛛的三个平面的距离自然可以计算出来。那么，这个点不是唯一确定的吗，它的位置是可以精确唯一表示的。
笛卡尔欣喜若狂。他在日记中写道:“第二天，我开始明白这个惊人发现的基本原理。”这时候他就有了代数和几何相结合的理论基础。
然后一发不可收拾。根据这种把数和形结合起来的思想，他创立了我们现在所说的“解析几何”。在平面上，用一个点到两条固定直线的距离来描述一个点在空间中的位置，用一个点到三个相互垂直的平面的距离来精确定位该点。这时，几何问题不仅可以用代数形式表示，还可以用代数变换来实现其几何性质。
解析几何的出现具有跨时代的重要意义。它改变了自古希腊以来几何与代数分离的趋势，完美地统一了数与形这两个对立的概念，将几何曲线与代数方程结合起来。这一天才的创新为微积分的创立奠定了基础。
上一篇：42式太极剑肖勇分段教学下一篇：历届辽宁女排队员名单
相关文章
- 详细阅读
-
四大洋的面积排序是怎样的详细阅读
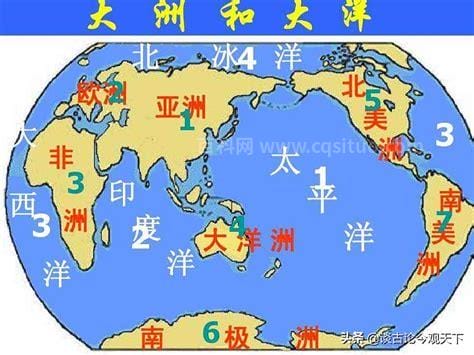
四大洋的面积排序是怎样的很多小伙伴都不知道如何解决这个令人困扰的问题，下面的，这几件事容易考不好希望大家能找到问题的答案！& nbsp & nbsp地球上的海洋面积为3.61亿平方公里，占地球总表面积的71%，海洋分为四大洋，即太平
2023-10-13 16:22:01
-
孩子需要怎样的暑假，暑假怎样安排孩详细阅读
生活中很多朋友不懂得孩子需要怎样的暑假，这个问题小编觉得还是比较简单的，亲自了解了一下后，就给大家带来了这篇文章，目的当然是能够帮助所有朋友，具体来看下。孩子放暑假后，家长的担心越来越多，脱离了老师的控制。幼儿非常
2023-10-13 14:39:52
-
千里鹰望远镜质量怎样详细阅读
千里鹰望远镜质量怎样这是最近困扰很多网友的一个问题吧，大家都不知道如果解决，相信大家看完这篇心中会有答案的，边看边学，让我们一起看一下吧。千里鹰望远镜品质卓越，光学精密，清晰度高，亮度高，手工质感。它是专门为远距离侦
2023-10-13 13:08:26
-
志愿者怎样查询志愿者证书详细阅读
志愿者怎样查询志愿者证书很多小伙伴都不知道如何解决这个令人困扰的问题，下面的，这几件事容易考不好希望大家能找到问题的答案！先用搜索框搜索“中国志愿者查询”，搜索后找到中国志愿服务网-全国志愿服务信息系统的网址，
2023-10-13 12:54:01