生活中有许多的朋友最近问小编藏红花对男人性功能有帮助吗(藏红花含有活性成分/但是缺乏充足的科学研究证明其功效)的问题,那小编收集整合后,今天为大家分享关于的相关文章,一起来了解一下吧!1.藏红花含有活性成分。藏红花
2023-10-27 03:48:02

证明费马大定理(证明过程详解)
已知:A 2+B 2 = C 2
设c=b+k,k = 1.2.3...,则a 2+b 2 = (b+k) 2。
因为整数c必须大于A和B,并且至少大于1,所以k = 1.2.3...
设:a = d (n/2),b = h (n/2),c = p (n/2)。
那么a 2+b 2 = c 2可以写成d n+h n = p n,n = 1.2.3...
当n=1时,d+h=p,d、h、p可以是任意整数。
当n=2,a=d,b=h,c=p时,则D2+H2 = p2 = > a2+B2 = C2。
当n≥3时,a 2 = d n,b 2 = h n,c 2 = p n。
因为,A = D (n/2),B = H (n/2),C = P (n/2)要保证D,H,P都是整数,就要保证A,B,C都是平方数。
∴a,b,c必须是整数的平方,这样d,h,p就可以是公式D N+H N = P N中的整数
如果D、H、P不能同时作为整数存在于公式中,费马大定理成立。
设a=mk,则b = k(m ^ 2-1)/2。
设m=k,则a = m ^ 2,b = m(m ^ 2-1)/2,设m/2 =(m ^ 2-1),则b = (m/2) 2,c = (m/2) 2+m。
那么a2+B2 = C2 = > M4+(m/2)4 =[(m/2)2+m]2 = > m2(2m ^ 2-m-2)= 0,m1=0(略)。
另外,当m/2 =(m ^ 2-1)时,(也可以让)b =(m ^ 2-1)2。
那么a2+B2 = C2 = > M4+(m2-1)4 =[(m2-1)2+m]2 = > m(m2-1)(2m 2-m-2)= 1
验证:当m = 1时,b = h (n 2) = (m 2-1) 2 = 0,即a 2 = c 2。不符合问题的要求。
如果d,h,p能以整数的形式出现,说明方程d n+h n = p n成立,但费马大定理不成立。否则D N+H N ≠ P N不等式成立,费马大定理成立。
费马大定理如何证明
费马大定理的证明过程:设a = d (n/2),b = h (n/2),c = p (n/2),那么a ^ 2+b ^ 2 = c ^ 2可以写成d ^ n+h ^ n = p ^ n,n=1。
1.若A、B、C均为大于0的不同整数,M为大于1的整数,若A M+B M = C M+D M+E M的同伦关系成立,则在A、B、C、D、E的比值增大后,同伦关系仍然成立。
证明:在定理的原公式中,a m+b m = c m+d m+e m,取增加比例为n,且n > 1。
得到:(na) m+(nb) m = (NC) m+(nd) m+(ne) m。
原来的公式是:n m (a m+b m) = n m (c m+d m+e m)
原公式是两边消去n m得到的。
所以同幂和差公式之间有一个增比计算规则,增比后还是同幂。
2.如果A、B、C是不同的整数且关系A M+B = C M成立,其中B > 1且B不是A、C的同次幂,当A、B、C同比增加时,B仍不是A、C的同次幂.
证明:取定理A M+B = C M的原公式。
当增加率为n,且n > 1时,我们得到:(na) m+n MB = (NC) m。
原来的公式是:n m (a m+b) = n MC m。
原公式是两边消去n m得到的。
既然b不能转化为a和c的同次幂,n^mb也不能转化为a和c的同次幂.
因此,在同次幂和差之间不是同次幂的项的比率一起增加后,等式关系仍然成立。
其中,同次幂项增加比例后仍为同次幂,非同次幂项增加比例后仍为同次幂。
相关文章

生活中有许多的朋友最近问小编藏红花对男人性功能有帮助吗(藏红花含有活性成分/但是缺乏充足的科学研究证明其功效)的问题,那小编收集整合后,今天为大家分享关于的相关文章,一起来了解一下吧!1.藏红花含有活性成分。藏红花
2023-10-27 03:48:02
生活中有些小伙伴会遇到48小时核酸证明怎么开提前几天做的问题,没有关系,通过这篇文章就能帮大家轻松解决,跟着小编我们一起来看下正文。目前疫情期间,出远门需要有核酸检测阴性结果报告,所以很多人想知道48小时核酸证明怎
2023-10-22 15:27:01

女生有腹肌好吗很多小伙伴都不知道如何解决这个令人困扰的问题,下面的,这几件事容易考不好希望大家能找到问题的答案!有腹肌的人一般身材都很好。长期锻炼的人有两个目标。一是保持健康,二是保持优越的身材。和男生相比,女
2023-10-15 15:54:02
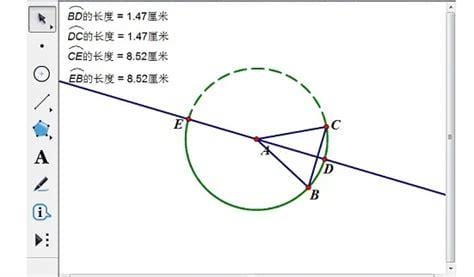
最近很多朋友都遇到了垂径定理五个条件的问题,今天小编就来为大家解答,快来看看吧。1.平分弦对面的弧 2.平分弦对面的另一条弧。将弦一分为二4.垂直于弦 5、通过圆心(或直径)只要满足任意两个条件,就可以得出另
2023-10-14 05:15:01

大家在生活的过程中总会遇到一些问题,比如哲罗鲑吃人吗,那么今天小编就为大家分享关于的相关文章,希望在这篇文章中你能了解到相关内容。哲罗鱼又称哲罗鱼,是一种冷水性淡水肉食性鱼类,主要分布于亚洲北部,在我国的黑龙江
2023-10-13 13:39:54