生活中,很多小伙伴不知道痔疮一期二期三期图片?今天小编针对这个问题做了这篇文章,详细内容我们来看一下。1、混合痔可以自愈对吗2、内痔三期要怎么治疗痔疮内痔怎么治估计的了3、痔疮到什么程度要手术4、得了痔疮有哪
2023-12-01 08:00:01

纳什均衡:在非合作博弈中,存在一个策略组合,使得每个参与人的策略更好地回应其他参与人的策略。如果参与者目前选择的策略形成了“纳什均衡”,那么对于任何一个参与者来说,单方面改变自己的策略都不会带来任何好处。
上面这段话值得一读。看完例题可以多看几遍。
具体例子如下:囚徒困境、智能猪博弈、范式博弈、饿狮博弈、硬币正反博弈。
囚犯的困境假设两个小偷,A和B,因入室盗窃被捕。警察把他们放在不同的房间进行审讯,并给出了如下政策:如果一名嫌疑人供认并交出赃物,两人都将被定罪。如果另一名嫌疑人也供认不讳,他们每人被判处8年徒刑;如果另一个犯罪嫌疑人否认,他将被判处另外两年的监禁,而忏悔者将被立即释放。如果两人都否认,盗窃证据不足,但会以非法侵入罪各判一年有期徒刑。即:
表中数字分别代表A和B的量刑结果。此表一般用于博弈论分析。
这时候有人会觉得双方都否认就好,但问题是双方都被孤立了,会怀疑对方为了保护自己而背叛自己。
两个人会怎么想?
如果对方坦白,这个时候,如果我不承认,我要坐10年牢,如果我坦白,我要坐8年牢;如果对方否认,如果我这时候也否认,就判一年,如果我坦白,就可以释放。基于以上考虑,不管对方坦白与否,我坦白更划算。这时候最后的“纳什均衡”只能是两个人坦白,一起被判八年有期徒刑。
智猪博弈猪圈里有两头猪,一头大猪和一头小猪。猪圈的一侧有一个踏板。每踩一次踏板,就会有少量的食物落在猪圈另一侧远离踏板的喂食口。如果一只猪踩在踏板上,另一只猪有机会先吃掉掉在另一边的食物。但当小猪踩下踏板时,大猪刚好会在小猪跑到食槽前吃完所有的食物;当大猪踩下踏板后,在小猪吃完掉下来的食物前,有机会跑到食槽,试着吃掉另一半。
那么,两只猪会采取什么策略呢?
当然,小猪在食槽边等着,而大猪在踏板和食槽之间不知疲倦地奔跑着。因为,小猪不蹬会什么也得不到,不蹬却能吃到食物。对于小猪来说,不管大猪踩不踩踏板,不踩总是一个不错的选择。另一方面,大猪知道小猪不会踩踏板,自己踩总比不踩好,只好踩。
范式博弈GOO公司和SAM公司是利益关系,他们的收益会随着游戏的变化而变化。如下图所示:
双方都有“合作”和“背叛”两种可选策略,网格中的四组数据分别代表了四种博弈结果各自的收益。每组数据的第一个数字代表GOO公司的收入,后一个数字代表SAM公司的收入。
现在我们从GOO的角度来思考整个游戏策略。如果山姆选择合作,那么我们合作的收益是3,我们背叛的收益是5,所以我们应该选择背叛;如果山姆选择背叛,那么我们合作的收益是-3,我们背叛的收益是-1,所以我们还是应该选择背叛。
同样,山姆也会做出同样的选择。最后我们发现这个博弈双方都采取了背叛策略,各自的收益都是-1,这是一个比较糟糕的结局,虽然对任何一方来说都不是最糟糕的那种。
但是,游戏次数往往不止一次。当两家公司经历了多次背叛策略的博弈后,发现公式中也有(3,3)收益的双赢,显然要好得多。因此,两家公司在随后的博弈过程中必然会试图建立互信,从而驱使双方选择合作策略。
但如果双方都知道游戏次数有限,也许下一局就是最后一局,那么为了避免上一局对方背叛造成-3的损失,双方都会采取背叛策略,最终游戏结果会回到(-1,-1)。
这样,随着时代的变化,博弈的性质也会发生变化,纳什均衡点也会发生变化。
饿狮博弈假设有A、B、C、D、E、F六只狮子(实力从左到右排序)和一只羊。假设A吃完羊会睡午觉,那么比A稍弱的B会趁机吃A,然后B会睡午觉,然后比B稍弱的C会吃B,以此类推。问:狮子A敢吃羊吗?
问题一定要逆向分析,从最弱的F开始,依次推进。假设E睡着了,F肯定会吃掉E,因为F后面没有其他狮子,不用担心被吃掉。继续往前推,既然E知道她睡着了会被F吃,那E肯定不敢在她睡着的时候吃D。既然E不敢吃D,D就可以放心吃睡C。依次往前推,得到C不吃,B吃,A不吃。所以答案是狮子A不敢吃羊。
但是,如果我们在狮子F后面加一个狮子G,总数变成7,用逆向分析按照上面的步骤再推一次,如下图。这次的答案变成了狮子A敢吃羊。
对比两个游戏,我们发现狮子A敢不敢吃羊,取决于狮子总数的奇偶性:当总数为奇数时,A敢吃;当总数为偶数时,A不敢吃。因此,奇数狮子和偶数狮子之间的博弈形成了两个稳定的纳什均衡点。
硬币正反博弈假设你和一个美女玩数学游戏。美女的建议:让我们各自展示硬币的一面。如果我们都是人头,那我给你3块钱;如果我们都是尾巴,我给你1块钱;剩下的你给我,2块钱。那么该不该和这个美女玩这个游戏呢?
这里我们需要谈谈纳什均衡的分类:
(1)纯策略纳什均衡,也就是说玩家可以采取固定的策略(比如总是玩正面或者总是玩反面),让每个人都赚得最多或者损失最少。
(2)混合策略的纳什均衡是给每个纯策略分配一个概率而形成的策略。混合策略允许玩家随机选择一个纯策略。混合策略纳什均衡要用概率计算,当达到一定概率时,支付可以更好。因为概率是连续的,所以即使策略集是有限的,也会有无限多的混合策略。
在这个博弈中,应该采用混合策略纳什均衡。
假设我们正面的概率是x,我们反面的概率是1-x,我们美女正面的概率是y,我们反面的概率是1-y,为了利益最大化,无论对手是正面还是负面,我们都应该是平等的,即:
3x + (-2)(1-x) = (-2) * x + 1*(1-x)
解方程x = 3/8;
同理,美女的收益:-3y+2(1-y) = 2y+ (-1) * (1-y),
解方程时y等于3/8。
所以我们可以算出美女的期望收益是:(1-y)*(2x-(1-x))+y(-3x+2(1-x))= 1/8元,也就是说如果双方都采取更好的策略,美女平均每次都会赢1/8元。
所以你当然不能和她玩这个游戏。其实只要美女采用(3/8,5/8)的方案,无论你采用什么方案,都改变不了局面。
但是当你也采取更好的策略时,你至少可以保证你损失最小。否则,你会失去更多。
相关文章
生活中,很多小伙伴不知道痔疮一期二期三期图片?今天小编针对这个问题做了这篇文章,详细内容我们来看一下。1、混合痔可以自愈对吗2、内痔三期要怎么治疗痔疮内痔怎么治估计的了3、痔疮到什么程度要手术4、得了痔疮有哪
2023-12-01 08:00:01

生活中的许多朋友最近问小编上海干冰多少钱☢一斤的问题,那么小编收集整合后,今天为大家分享关于的相关文章,一起来了解一下吧!起始:1、混合气体灭火器价格是多少2、炎热的夏天上海比海门温度高,这是由于上海3、下雨人工降
2023-11-27 18:40:02

在生活的过程中总会遇到一些问题,比如黄瓜减肥法一周瘦20斤,那么今天小编就为大家分享关于的相关文章,希望在这篇文章中你能了解到相关内容。起始:1、瘦身期间三餐吃什么2、吃黄瓜一周能瘦多少斤3、什么样的减肥方法最
2023-11-27 13:00:02

生活中有许多朋友问小编引人入胜的酒类销售策略优质,那么今天小编就为大家解决一下这个问题,希望对你有所帮助。诱人的酒类销售策略是指吸引人们的注意力和品味,促使他们购买各种酒类产品的战略方法。在当今激烈竞争的市
2023-11-27 01:16:01
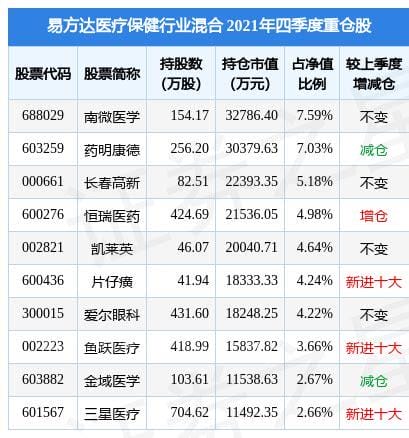
易方达医疗保健行业混合盘中的估值情况优质是各位朋友所需要解决的问题,问题理解之后可以给朋友带来很大的帮助,所以今天小编就给大家带来的详细讲解,一起来看看吧。近日,易方达健康医疗行业估值备受关注。最新数据显示,基
2023-11-26 10:16:01