为什么正多面体只有5种

生活中很多朋友不懂得为什么正多面体只有5种，这个问题小编觉得还是比较简单的，亲自了解了一下这个问题后，就给大家带来了这篇文章，目的当然是能够帮助大家，具体来看下。

1.证明:设正多面体的每个面都是正n边行，每个顶点都是m条边，那么边数E应该是f(面数)和n的乘积的一半，即NF = 2e(公式1)。同时e应该是v(顶点数)和m乘积的一半，即mv = 2e(公式2)。从公式1和公式2，得到f = 2e/n和v = 2e/m。将它们代入欧拉公式V+F-E=2，用2E/m+2E/n-E=2排列，得到1/m+1/n = 1/2+1/e

2.由于E是正整数，1/E>0。所以1/m+1/n > 1/2(公式3)，公式3说明m和n都不能大于3，否则公式3不成立。另一方面，由于m和n(正多面体一个顶点的边数和多边形的边数)的含义，m>=3，n>=3。所以m和n中至少有一个等于3。

3.当m=3时，因为1/n > 1/2-1/3 = 1/6，n是正整数，所以n只能是3，4，5。

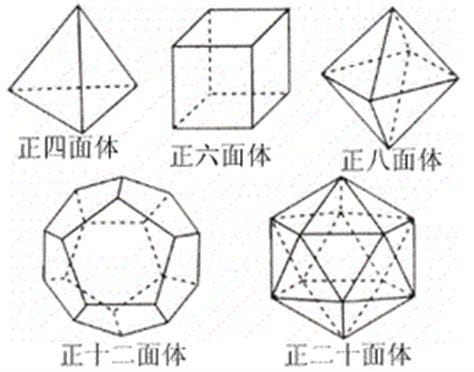
4.同样，n=3，m只能是3，4，5，所以只有nm型的五种正多面体，33个正四面体，43个正六面体，34个正八面体，53个正十二面体，35个正二十面体，因为以上五种多面体可以用几何方法制作，但不可能有其他种类的正多面体。