量子力学通俗讲解不等式（为什么证明贝尔不等式不成立）

今天小编给各位分享量子力学通俗讲解不等式（为什么证明贝尔不等式不成立），如果能碰巧解决你现在面临的问题，别忘了关注小站，我们一起开始吧！

北京时间10月4日，2022年诺贝尔物理学奖被授予法国物理学家阿兰·塞西(Alain Aspect)、美国理论和实验物理学家约翰·弗朗西斯·f·克劳斯(john francis F. krause)和奥地利物理学家安东·泽林格(Anton Zeilinger)，以表彰他们在量子信息科学研究方面的贡献。他们通过光子纠缠的实验，确定了贝尔不等式在量子世界不成立，创立了量子信息这门学科。

澎湃科技连线多位量子信息领域的科学家，解读三位诺奖得主的学术突破性贡献、研究意义和当前发展。

2022年诺贝尔物理学奖得主:法国物理学家阿兰Aspect、美国理论和实验物理学家约翰·弗朗西斯·f·克劳斯和奥地利物理学家安东·泽林格图片来源:诺贝尔奖委员会官网。

澎湃技术:你之前准确预测了2022年诺贝尔物理学奖的三位得主。当时为什么会做出这样的预测？

彭雪(北京计算科学研究中心教授):这三位科学家因其对量子物理的基本概念和实验的贡献获得了2010年的沃尔夫奖。比如《科学内幕》连续三年预测他们可能获得2019年、2020年、2021年的诺贝尔物理学奖。我也认为他们应该得到这个奖。

澎湃技术:物理学界对今年诺贝尔物理学奖的量子信息有什么反应？这是意料之中的吗？

金宪民(上海交通大学物理与天文学院教授):最近的国际重大科学事件确实集中在量子信息领域。比如今年上半年举行的第28届Solvey物理大会的主题就是量子信息的物理。上个月，基础物理学突破奖授予了量子信息领域的查尔斯·贝内特、吉尔斯·布拉萨尔、大卫·多伊奇和彼得·肖尔，以表彰他们在量子信息领域的基础工作。今年的诺贝尔物理学奖花在量子信息上并不奇怪。

兀术(华东师范大学-阿尔伯塔大学高等科技学院执行院长):这是很多人所期待的。近年来，量子信息技术发展迅速，并逐渐实用化，为人类社会做出贡献，这也是诺贝尔奖设立的初衷。所以大家都期待量子信息在近几年的诺贝尔物理学奖中有所收获。

澎湃技术:如何评价这三位科学家的突破性贡献？

彭雪:总的来说，这三位科学家都从实验上验证了违反贝尔不等式，从而证明了量子力学的完备性。

当初爱因斯坦和哥本哈根学派有一场争论——量子力学是否完备。没有人认为量子力学是错误的，但关于它是否完整的争论由来已久。而爱因斯坦则希望将量子力学中的一些现象与宏观世界中的一些现象进行比较，比如涉及到局域实在论的贝尔不等式。宏观世界中存在局部现实，比如宏观世界中所有的相互作用都与距离有关，距离越远，相互作用越弱。量子力学没有定域性，比如量子纠缠就属于量子非定域性。所以，当人们对定域性和非定域性没有清晰的认识时，就会认为量子力学是不完整的，会有很多争议。

后来大卫·玻姆在1952年通过引入“隐变量”理论做了非常好的解释，在局域实在论的基础上形成了完全决定性的理论——局域隐变量理论。他认为一个隐藏的变量在操纵着整个量子世界看似不可思议的事情，但他不知道这是一个什么样的变量。贝尔定理的实验验证是一个物理实验，旨在检验量子力学理论或局域隐变量理论是否正确。1964年，约翰·贝尔定义了一个可观测的测度，并基于局部隐变量理论，预言测量值不超过2。用量子力学的理论，可以得到大于2的测量值。一旦实验测量结果大于2，就说明局部隐变量理论是错误的。

在宏观世界中验证贝尔不等式，总会得到贝尔不等式。那么，这意味着量子力学是不完整的。后来这三位科学家相继用实验验证了在量子力学框架下贝尔不等式会被违反，量子力学才算完整。

兀术:三位科学家在验证贝尔不等式方面的突破性贡献为量子信息技术的建立奠定了基石。

艾伦·阿斯佩(Alan Aspe)在实验中用一种新的方式激发原子，这种方式可以以更高的速率发射纠缠电子。同时，他可以切换实验参数，这样实验系统中就不会有提前信息影响实验结果。

尹(北京理工大学物理学院量子技术研究中心教授):约翰·克劳萨、艾伦Aspect和安东·蔡林格的研究直击量子力学的核心基础问题，从实验上验证了贝尔不等式。

贝尔不等式的根源来自于1935年爱因斯坦、波多斯基和罗森提出的一个悖论，即EPR(爱因斯坦-波多斯基-罗森)悖论:要么量子理论不完备，要么量子力学会导致超光速作用，这与定域性相反。EPR佯谬质疑的不是量子力学的正确性，而是量子力学的不完全性。

1964年，英国物理学家约翰·贝尔定义了一个可观测的测量，并基于局部隐变量理论，预言测量值不超过2。但是用量子理论可以得出最大值可以达到2√2。一旦实验测量结果大于2，就说明局部隐变量理论是错误的。贝尔一直站在爱因斯坦一边。贝尔研究隐变量理论的初衷是为了证明量子理论的非定域性是错误的，但后来所有的实验都表明定域隐变量理论的预言是错误的，量子理论的预言与实验是一致的。贝尔不等式的诞生，宣告了量子理论的局部争议从带有哲学色彩的纯理论思辨，转变为带有实验可证伪性的科学理论。

约翰·克劳斯证明贝尔不等式的实验不成立:钙原子被特殊光激发，发出两个纠缠光子，然后用两端的滤光片测量其偏振。

约翰·克劳萨发展了贝尔的想法。1972年，约翰·克劳萨等人完成了第一个贝尔定理实验。由于局域化漏洞，即纠缠粒子之间的距离太小，无法解释纠缠的非局域性，所以结果不具有说服力。

1982年，艾伦Aspect等人改进了克劳萨的贝尔定理实验，实验结果违反了贝尔定理。

1998年，Anton Zeilinger等人在奥地利因斯布鲁克大学完成了贝尔定理实验，彻底消除了局域化的漏洞。实验结果是决定性的。

2015年，安东·蔡林格完成了贝尔不等式无漏洞的实验验证，同时排除了定位漏洞和测量漏洞。

澎湃技术:诺贝尔物理委员会主席安德斯·伊尔贝克(Anders Irbä ck)表示“获奖者对纠缠态的研究非常重要，甚至超越了解释量子力学的基本问题”。这句话怎么理解？

金贤敏:量子纠缠是一种神奇的现象。纠缠对中一个粒子的情况决定了另一个粒子的情况，即使它们相距很远。长期以来，学术界争论的是关联是否是因为纠缠对中的粒子含有隐变量，这些指令告诉它们在实验中给出哪个结果。20世纪60年代，约翰·斯图尔特·贝尔发展了一个以他的名字命名的数学不等式。这说明，如果存在隐变量，大量测量结果之间的相关性永远不会超过某个值。然而，量子力学预测，某种类型的实验将违反贝尔不等式，导致比本来更强的相关性。

在纠缠量子态中，即使两个粒子分开，它们的行为也像一个整体。2022年诺贝尔物理学奖获得者的研究成果为基于量子信息的新技术扫清了道路。

彭雪:纠缠是量子信息中最重要、最基本的单元，比如量子保密通信、量子通信、量子计算等等，都是基于量子纠缠的。正是因为量子纠缠的独特性质——量子非局域性，它才能拥有一些完全超越经典物理的功能。其次，还提供了量子纠缠光源的大规模制备方法和量子纠缠光源的高亮度制备方法，可以确认量子纠缠光源的有效性。

吴石:用纠缠光子验证贝尔不等式不仅是量子力学基本问题的解决，也是纠缠态在量子通信和量子精密测量中的应用。

尹:量子信息技术的理论基础几乎都是基于量子非局域性或者量子纠缠。量子网络和量子计算机与量子纠缠有很深的关系。这也意味着他们的工作为基于量子信息的新技术扫清了道路，有利于未来全量子网络和量子计算机的发展。

澎湃技术:他们在光子纠缠的实验研究中克服了哪些困难？

金贤敏:早在2010年，就有三位科学家凭借基于量子物理的基本概念和实验贡献，尤其是一系列日益复杂的贝尔不等式测试，获得了沃尔夫奖。今年的诺贝尔奖是“表彰他们对纠缠光子的实验，证明了贝尔不等式的违反，开创了量子信息科学”。具体来说:

阿兰看点:他在做博士论文的时候，他带领团队的实验证实了贝尔定理的正确性，说明了爱因斯坦、波多尔斯基、罗森论文中的“荒谬”，即当两个粒子相隔任意距离时，“远距离的鬼效应”似乎已经在现实中实现了:两个粒子的波函数之间的相关性仍然存在，因为它们曾经是同一个波函数的一部分，在测量其中一个之前，它们并没有受到干扰。

约翰·克劳斯:他读了著名的EPR佯谬论文和玻姆的“隐变量”论文。1967年，他进一步阅读了贝尔的论文。他意识到贝尔定理可以通过实验来检验。中间遇到了很多困难，但我一直在这个方向上坚持研究，最终与伯克利的查理·汤斯合作进行了一项实验，实现了当初困扰爱因斯坦的幽灵般的远距离效应。

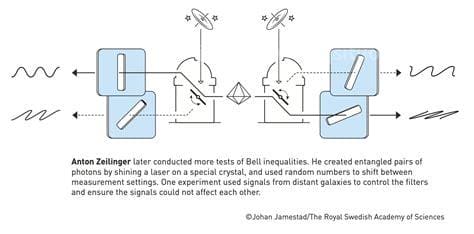
安东·塞林格进行了更多的实验来证明贝尔不等式不成立。他用激光照射特定的晶体来产生纠缠光子对，并在测量中使用随机参数。他的研究团队证明了量子隐形传态现象，量子态可以从一个粒子转移到远处的另一个粒子。

安东·蔡林格(Anton Zeilinger):他以纠缠的实验和理论工作而闻名，最著名的是多粒子纠缠态的实现、量子隐形传态、量子通信和密码学以及光子量子计算。1997年，他和同事首次完成了量子隐形传态的理论实验验证，成为量子信息实验领域的一个创举。

吴石:光子纠缠的实验发展受到很多实验技术和仪器的限制。在早期的实验中，由于纠缠光子对的低效率、光子探测的低效率和光子探测的高噪声，很难读出有效的光子信息，所以光子的量子特性很难呈现给大家。这三位科学家通过巧妙的设计实验，发展出不同的方法来产生纠缠光子对，克服各种不利条件，尽可能地贴近理论假设，并在实验中验证了贝尔不等式的失败。

彭雪:首先是光源的困难。因为纠缠光子对或纠缠离子对肯定会违反不等式，所以很难找到和制备这样的粒子。准备完后，如何堵住实验漏洞，比如相关的本地化漏洞，能不能相差很远，这也是实验的难点。同时，他们的实验验证本身就是开创性的。

澎湃技术:具体来说，这三位科学家有哪些标志性的成就？

彭雪:安东·泽林格在1997年完成了量子隐形传态的实验验证，并首次通过实验实现了量子隐形传态。这篇论文发表在《自然》杂志上，并入选历史上最有影响力的100篇文章。

当约翰·克劳萨与迈克尔·霍恩、阿布纳·希莫尼和理查德·霍尔特一起在哥伦比亚大学读研究生时，贝尔在1964年的数学定理通过现在称为克劳萨-霍恩-希莫尼-霍尔特(CHSH)的不等式转化为一个非常具体的实验预测。

之后，约翰·克劳斯(John krause)与研究生斯图尔特·弗里德曼(Stuart Freedman)一起，首次证明了相距甚远的两个粒子可以纠缠在一起。约翰·克劳萨继续进行了另外三个实验来测试量子力学和纠缠的基础，每个新的实验都证实并扩展了他的结果。弗里德曼-克劳萨实验是对CHSH不等式的第一次检验。它已经在世界各地的实验室中测试了数百次，以确认量子纠缠的真实性。

兀术:首先，艾伦·阿斯佩首先在精确意义上验证了贝尔不等式，证明了量子论的正确性。其次，Alain Aspe首次实现了单光子的干涉实验，验证了单光子的波粒二象性。第三，Alan Aspe首次比较了费米子和玻色子的二阶关联。

纠缠粒子对中一个粒子的状态决定了另一个粒子的状态，即使这两个粒子相距很远。

澎湃技术:在量子信息领域，目前最受关注的核心问题是什么？

金贤敏:量子信息主要包括三个方向:量子计算、量子通信和量子精密测量。量子力学对微观粒子的结构、性质和相互作用的研究和表征，与信息论一起，为信息获取、处理和传输技术的发展和应用奠定了基础，成为连接物质、能量、信息等基本要素的桥梁和纽带。

在这三个方向中，量子计算潜力最大，正在成为新一轮科技革命的核心科技力量。量子计算以量子比特为基本单位，利用量子叠加和干涉原理实现并行计算，可以提供指数级加速，实现突破经典计算极限的计算能力飞跃。与传统计算机相比，量子计算具有超高计算能力、并行计算和可逆计算的特点。可用于人工智能、电信网络、航空航天、金融科技等领域。随着量子计算算法和应用的不断拓展，有可能在量子化学、组合优化、复杂网络测序等领域率先取得突破。

彭雪:一定是量子计算。量子计算是一个比较遥远的方向，最难也最有意义。另外，比如量子保密通信、量子精密测量都是应用到量子纠缠的特性，这也是我们关注的问题，可能会产生一些改变人类生产生活方式的应用。

兀术:目前量子信息领域有几个核心问题:量子通信、量子模拟、量子传感和量子计算。

澎湃技术:在实现真正的量子计算机之前，你认为需要解决哪些核心科学问题？

金贤敏:近年来，量子计算硬件物理平台的各种技术路线的比特数和量子量都创新高，但仍处于并行发展阶段，技术路线没有趋同的趋势。目前国际公认的主流方向有三个:超导、离子阱、光量子。其中超导量子计算机的运行环境需要接近绝对零度，这就需要高温，离子阱的量子计算需要超高真空和一定的低温环境。实现一台通用量子计算机有三个前提条件——百万量子比特的操控能力、低环境要求和高集成度。光量子路径是唯一能满足这些条件的技术体系，是大规模通用量子计算最可行的路径。

彭雪:首先是大规模量子纠缠的制备。另外，要真正做量子计算，可能需要让多个粒子处于纠缠态，也就是如何制备多粒子纠缠。此外，还需要保持其连贯的特性，使其寿命变得很长。因为量子的所有特性都是基于它的叠加特性，如果一个外界的干扰，或者说噪声，消除了它的相干性，那么它就失去了量子纠缠的特性，无法应用于量子计算。所以非常稀有，也非常容易被破坏。

兀术:要实现通用量子计算机，目前要解决的核心科学问题是实现量子比特的大规模制备和操纵。

,