许多生活朋友不知道麦当劳汉堡包之谜,麦当劳传说故事,对此很疑惑,那么今天就和小编一起来看看吧,一定可以帮助到你。1、麦当劳传说故事麦当劳的传奇源于理查德·麦克唐纳和莫里斯·麦克唐纳两兄弟的创业过程。据说他们在
2024-01-09 09:48:02

关于数学家的小故事
罗庚(1910-1982)出生于江苏太湖之滨的金坛县。他被命名为罗庚,因为他出生时被他的父亲华老乡放在洗衣单上以求好运。
华从小贪玩,也喜欢凑热闹,但功课平平,有时不及格。勉强读完小学,进了老家的金坛中学,但还是贪玩,字写得歪歪扭扭。我做数学作业的时候,画的很仔细,但是就像涂鸦一样。因此,初中时的华仍然不被老师喜欢,经常被统治。
金坛中学教师王维科眼光独到。他研究了华的涂鸦本,发现这些被涂改的地方反映了他在解决问题时探索的各种方法。有一次,王维可老师告诉他的学生【孙子兵法计算】有这样一个问题:“今事未知,三三数为第二,五五数为第三,七七数为第二。事物的几何是什么?”当所有人都沉默的时候,一个学生站了起来。大家一看,原来花一直被人看不起。那时候,他才十四岁。你能猜出华说了多少吗?
16世纪的德国数学家鲁道夫,一生都在计算圆周率到小数点后35位,后来被称为鲁道夫数。他死后,别人把这个数字刻在他的墓碑上。瑞士数学家雅克·伯努利(Jacques Bernoulli)生前研究过螺旋(被称为生命之线)。他死后,墓碑上刻了一条对数螺线,碑文还写着:“虽然我变了,但我和以前一样。”这是一句双关语,不仅描述了螺旋性质,也象征了他对数学的热爱。
华上小学的时候,一个老师给新老师介绍学校的时候,说这个学校的学生都是穷孩子,大部分都是傻逼...这深深地刺痛了华的心,他决心以优异的成绩回报老师。
有一天,数学老师给我们出了一个有趣的问题:今天有一个东西,它的数字是未知的,三三两两,五五三两,七七两。几何是什么?
全班面面相觑,答不上来。只有华站起来说:“老师,我知道是‘23’。”全班震惊,老师点头称赞。从此,他爱上了数学课。
华的故事都值得我们学习。在他读书的时候,父亲的店铺生意越来越差,他不得不辍学去看看柜台。他开始自学,用一本代数书,一本几何书,一本微积分书,只剩50页了。白天没时间,晚上守着小油灯反复计算。父亲骂他是“书呆子”,几次逼他烧书,邻居都劝他好好做生意。一些上大学的同学对他也有点冷淡。不幸的是,他又患上了可怕的伤寒,医生摇头叹息,让家人为他准备“葬礼”。他向死亡挑战,挣扎着在地里干活,左腿被摔成了残疾。他毫不畏惧,拄着拐杖锻炼,忍受着疼痛。练够了,他去了一所中学,给老师打杂,打水,削铅笔。即便如此,他也没有放弃自学。中学工作不久,他就开始给报刊杂志发数学论文,多次被拒后也不死心。后来他发表了《苏嘉菊代数五次方程的解为什么不能成立》一文,得到了数学大师熊庆来的赏识,很快被引进清华校园,放在身边。
一年半后,华修完了清华大学数学学院的所有课程,自学了英语和法语。然后,他的数学论文在国内外期刊上发表。1934年,经熊庆来推荐,华被任命为数学系助教。不久,学校领导任命他为数学教授。
一个贫穷的残疾人,最终以惊人的毅力自学成才,成为国内外著名的数学家。华的故事值得我们学习。
高斯(1777 ~ 1855),德国著名科学家,出生于一个贫穷的家庭。高斯在会说话之前就学会了自己计算。三岁时,他有一天晚上看父亲计算工资,纠正父亲的计算错误。
一天,高斯的数学老师很沮丧。他对同学们说:“你们今天给我算一下,从1加2加3到100的总和。谁想不通就罚谁不回家吃午饭。”
结果不到半个小时,小戈斯就拿起石板,走上前去。“老师,这是答案吗?”
老师头也没抬,挥了挥厚厚的手说:“走,回去算!不对。”
高斯站着不动,把石板放在老师面前:“老师!我认为这个答案是正确的。”
数学老师想吼,但当他看到石板上写着的数字:5050时,大吃一惊。这个8岁的孩子怎么这么快就得到答案?
高斯解释了他发现的一种方法,古希腊人和中国人都用这种方法来计算数列1+2+3+…+n,高斯的发现让老师感到羞愧,觉得自己以前那种傲慢自大,贬低穷人家孩子的观点是错误的。他以后也很认真地教书,经常从城里买一些数学书供自己学习,借给高斯。在他的鼓励下,高斯后来在数学方面做了一些重要的研究。
南宋数学家秦于1247年完成了《数书九章》一书,其中《中国剩余定理》、三对角求积、秦算法(高次幂方程正根的数值解法)等是具有世界意义的重要贡献。
在中国数学史上,流传着一个“韩信带兵”的故事:韩信是汉高祖刘邦手下的一名将军。他骁勇善战,为汉朝的建立做出了卓越的贡献。据说韩信的数学水平也很高。他在点兵时,为了保守军事机密,不让敌人知道自己部队的实力,从1到3报数先令士兵,然后记下最后一个士兵报的数字。然后让士兵从1数到5,也记下最后一个士兵报的数字;最后让士兵从1数到7,记下最后一个士兵报的数字;就这样,他很快算出了自己军队的士兵总数,而敌人却永远也查不出自己军队有多少士兵。因为《孙子舒静》对这类问题的研究由来已久,但仅仅处于起步阶段,还远未完成。所以后人把这个命题及其解法称为“孙子定理”,主要是因为孙子的计算在处理这类问题上是超前的。其实想法的成熟度还有待提高。为了解决“孙子”问题,秦推广了“孙子问题”的解法,提出了“中国剩余定理”。经过长期的积累和潜心研究,秦于公元1247年写下了《数书九章》。这部中世纪的数学巨著在很多方面都有所创造,其中“求解一个同余组的大求导”和求解高次方程数值解的“正负平方抽取”更是具有世界意义的成果。正因为如此,在西方数学史著作中,解一个同余组的剩余定理被理所当然地称为“中国剩余定理”。
约瑟夫·路易斯·拉格朗日(1736-1813)是18世纪一位伟大的科学家。他在数学、力学和天文学方面都做出了巨大的历史贡献,但在数学方面的成就最为突出。拿破仑曾称赞他是“数学领域中高耸的金字塔”,他最突出的贡献是在将数学分析的基础从几何和力学中分离出来方面起了决定性的作用。
拉格朗日出生在意大利都灵。作为长子,他的父亲希望他学习法律。然而,拉格朗日对法律毫无兴趣,热爱文学。直到16岁,拉格朗日仍然非常偏爱文学,对数学毫无兴趣。16岁时,他偶然读到一篇介绍牛顿微积分的文章,论分析方法的优点,这激起了他对牛顿的无限敬仰和敬仰,于是他下定决心要成为一名牛顿式的数学家。进入都灵皇家炮兵学院后,拉格朗日开始有计划地自学数学。由于努力学习,他进步很快,毕业前开始在这所学校教数学。20岁时,他被正式任命为该校数学副教授。从这一年开始,拉格朗日开始研究“极小极大”的问题。他采用了纯分析的方法。1758年8月,他给欧拉写信,讲述了自己的研究方法,欧拉给予了高度评价。从此两位大师开始频繁交流,在这一过程中诞生了一门新的数学分支——变分法。1759年,在欧拉的推荐下,拉格朗日被提名为柏林科学院通讯院士。然后,他被选为该院的外籍院士。在柏林科学院工作期间,拉格朗日对代数、数论、微分方程、变分法和力学进行了广泛而深入的研究。1813年4月10日,拉格朗日病逝,完成了他辉煌的科学之旅。他严谨的科学态度和精益求精的工作作风影响着每一位科学家。他的学术成就也为高斯、阿贝尔等世界著名数学家的成长提供了丰富的营养。可以说,在接下来的100年里,数学上的许多重要发现几乎都与他的研究有关。
相关文章

许多生活朋友不知道麦当劳汉堡包之谜,麦当劳传说故事,对此很疑惑,那么今天就和小编一起来看看吧,一定可以帮助到你。1、麦当劳传说故事麦当劳的传奇源于理查德·麦克唐纳和莫里斯·麦克唐纳两兄弟的创业过程。据说他们在
2024-01-09 09:48:02

有些小伙伴经常会碰到马保国的故事的问题,但是对于不是非常了解,给小伙伴带来了很多困惑,但小伙伴们找到这里算是没白来,因为小编就带大家详细讲解一下,具体内容如下。太极大师马保国是哪里人 太极大师马保国来自山东临沂
2024-01-06 11:54:01

生活中,有很多朋友觉得木头桩为什么谁都瞧不起很难弄明白,那么我们到底要如何解决这个问题呢,今天小编就带来大家看看,希望可以帮助各位。木头桩为什么谁都瞧不起 就是因为木桩自大,自以为比谁都聪明,所以没人看不起木桩。
2024-01-06 00:18:02

大家在生活的过程中会遇到很多问题,比如有些小伙伴对六尺巷在哪里不是很懂,不过没有关系,小编今天就给大家详细讲解一下这个问题,具体内容如下。六尺巷在哪里 1.柳池巷位于安徽省桐城市西南角,全长100米,宽2米。建于清朝康
2024-01-05 18:54:02
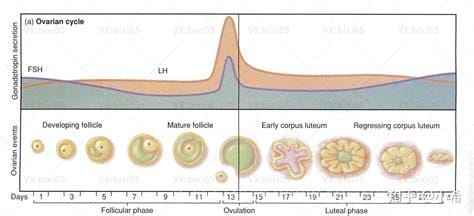
lh峰值后多久排卵希望不清楚的大家在这看一看,小编已经为大家把这个问题总结好了,希望接下来的能帮大家解决这个问题,看完了记得分享哦!lh峰值后多久排卵 排卵大约需要16.5小时。当然,每个人都会不一样。当卵泡发育到最后
2024-01-05 18:18:01