生活中有些小伙伴会遇到大基数是什么意思?的问题,没有关系,通过这篇文章就能帮大家轻松解决,跟着小编我们一起来看下正文。大基数一般指超重20斤及以上的人;小基数相对于大基数而言,差不多是超重10斤左右。男女体型基数的算
2023-10-25 06:21:01
一.概念描述
现代数学:定义自然数的方法之一。每个有限集合中元素的数量对应于一个自然数。在同一类有限集合中,它们有一个共同的特点,就是所包含的元素个数是相同的。比如三支铅笔、三头牛、三架飞机是同一类等价集合,它们的共同特征是3,数字3是它们的底数。所以,用来表示事物数量的自然数就是基数。一般来说,有限个对等体集合的共同特征称为这种对等体集合的基数。因此,有限集的基数是自然数。但自然数的集合是无限的,所有能与自然数集合建立一一对应关系的无限可数集合的基数被指定为0(读作Alef zero,希伯来语的第一个字母)。有了自然数的基数定义,我们就可以定义数的阶及其四则运算,建立自然数的基数理论,甚至建立自然数的公理系统。
小学数学:自然数有两层含义,当用来表示事物的数量时,称为基数;当用来表示事物的顺序时,称为序数。基数意义已经从数字1-5的识别开始,与数字的识别相结合,而序数意义是在理解数字1-5的基数意义的基础上学习的。
二。概念解释
基数的概念最早是由康托尔提出的,他在1874-1884年引入最原始的集合论(现在称为朴素集合论)时首次引入了基数的概念。他首先想到的是集合{l,2,3}和{2,3,4},这两个集合并不相同,但都有相同的基数。显而易见,为什么两组元素的数量是一样的?
康托尔的答案是所谓的一一对应,即两个集合的元素一一联系起来——如果能做到,两个集合的基数自然是一样的。虽然答案很容易理解,但它是革命性的,因为这种方法可以比较任意集合的大小,包括无限集合。他的定义是两个集合有相同的基数当且仅当它们是等势的。这个定义并不严格。没有说清楚“基数”是什么,只是指出了基数相等的充要条件。
后来弗雷格给出了基数的概念:集合X的基数为{y:y: y等于x}。(比如自然数1定义为{x:x: x是一元集合})。可以证明对于任意x,{y:y: y等于x}不是集合,而是真类。
后来,冯·诺依曼有了重大突破:他首先给出了一个严格的“序数”概念(康托尔等人的“序数定义”并不严格):序数是一个有序的传递集。在此基础上,他将基数的概念定义为:对于一个良序集合,X的基数是等势的序数中最小的。
到20世纪70年代,斯科特已经完全解决了这个问题。他发现了一个窍门——现在叫做“Scotttrick”,可以将任意类转化为指定子集,不需要选择公理,但必须使用ZF8(正则公理)。利用这个技巧,可以将乱序集X的基数定义为真类{y:y: y等于x}变换得到的集合。同时,斯科特证明了没有选择公理和规范公理就无法定义“基数”。也就是说,我们不能定义一个类函数F,使得对于任意一个集合x,y,F(x)=F(y),iffx与y是等势的。
最后,pincus证明了没有选择公理就不能定义一个类函数F,使得:①对任意集合X,Y,F(x)=F(y)iffx对Y是等位的;②对任意集合x,F(x)等于x..
至此,基数的定义完全解决了。
三。教学建议
(1)初步了解自然数作为基数的意义。
回答“有多少?”当时学生先数,再数到底,得出基数。在计数的过程中,他们必须沟通有序自然数与描述大小的自然数之间的对应关系(口中读出的数对应的是被计数的对象,即集合中的元素)。比如刘鹏老师在复习“认识10以内的数”的教学时,先给学生看了一张主题地图,然后问:“地图上有多少棵树?”当学生数出正确答案后,刘老师让另一名学生指着屏幕上的树,一棵一棵地数,让学生感觉到最后一棵树对应的数字6就是这一行的总树数。每棵树上有一只鸟,一共6只鸟。六棵树,六只鸟,它们的数字都是六,都可以用数字六来表示。
(2)经历基数概念的认知过程。
“基数”是一个相对抽象的概念。如何让一年级学生在第一学期充分感知和理解“10以内的数”,是大三教学中的一个重点和难点。当然,在教学中,教师要有意识地让学生亲身体验丰富的实践活动,把它们变成形象,通过让学生观察主题图、摆姿势、画图、转圈等方式,调动学生的手、脑、眼、耳、口协调运动。这既符合低年级学生的认知规律,又充分调动了学生学习的积极性和兴趣,从而使轻松学习变得困难,享受学习。课后要结合学生的生活实际进行适当的延伸,如让学生寻找身边的数字为1、2、3、4、5的物体,为学生在生活实践中进一步学习和巩固数学知识创造机会,同时加强学生对数学的应用意识,让学生多角度、多层次地理解“基数”的概念。
(3)正确理解自然数的基数和序数在特定语境中的含义。
因为自然数有两种不同的含义:基数和序数,所以一个句子中出现的自然数是基数还是序数要看具体的语言环境。比如学生在体育课上一字排开报号,头上是“1”,登记结束是“37”。这个“37”不仅意味着这个组有37个学生,还意味着组末的那个学生是第37个。
四。推荐阅读
(1)《小学数学研究》(张奠宙等,高等教育出版社,2009年)
第五章主要论述了数的起源、数系的扩展和数概念的发展史。
(2)《小学数学课堂的有效教学》(刘家峡,北师大出版社,2008)
本书从自然属概念的本质把握、教学方法、学习工具的使用等角度详细介绍了自然数的教学,对低年级的广大一线教师有一定的指导意义。
标签: 基数
相关文章

生活中有些小伙伴会遇到大基数是什么意思?的问题,没有关系,通过这篇文章就能帮大家轻松解决,跟着小编我们一起来看下正文。大基数一般指超重20斤及以上的人;小基数相对于大基数而言,差不多是超重10斤左右。男女体型基数的算
2023-10-25 06:21:01
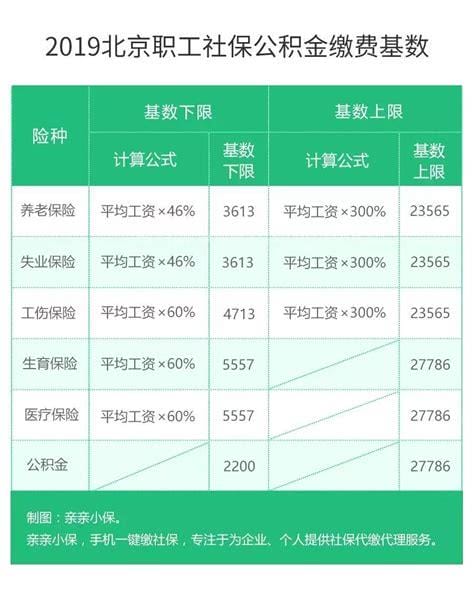
在生活的过程中总会遇到一些问题,比如北京市历年社保缴费基数一览表,那么今天小编就为大家分享关于的相关文章,希望在这篇文章中你能了解到相关内容。1.北京市养老保险最低基数为3613元,单位缴费比例为16%,个人缴费比例为
2023-10-14 14:51:26
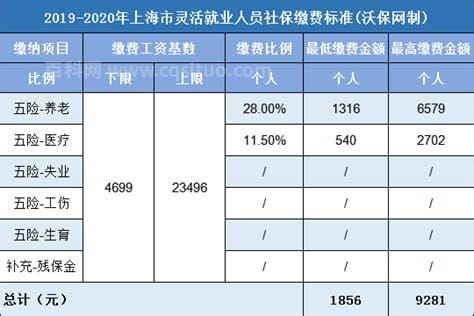
在生活的过程中我们经常会遇到许多的问题,就有朋友问小编有关的问题,那么今天小编就和大家来聊一聊,一起来看看吧。2014年上海市社会保障缴费规定养老保险缴费比例:用人单位21%,个人8%。养老保险缴费基数下限:3022元。养
2023-09-29 07:30:23
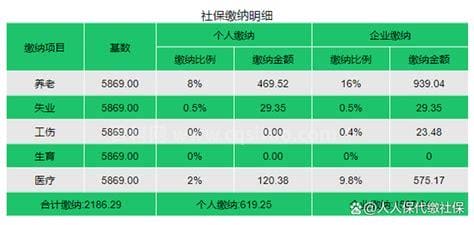
生活中很多朋友不懂得公积金缴费7000基数每月交多少,这个问题小编觉得还是比较简单的,亲自了解了一下这个问题后,就给大家带来了这篇文章,目的当然是能够帮助大家,具体来看下。公积金缴存比例不合法,企业可以在一定范围内浮
2023-09-08 00:38:01
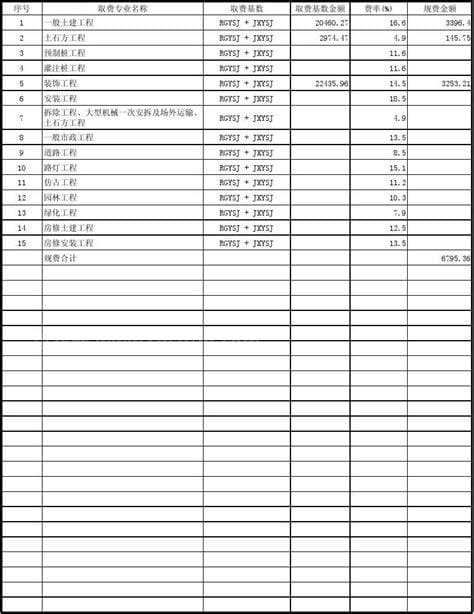
生活中很多小伙伴不了解规费计算方法和基数这件事,今天小编针对这个问题做了这篇文章,详细内容我们来看一下。费用有统一的计算公式。一般情况下,费用=计算基数*费率。但不同地区、不同地方对费率的规定不同,应该按照当地
2023-09-05 15:31:01