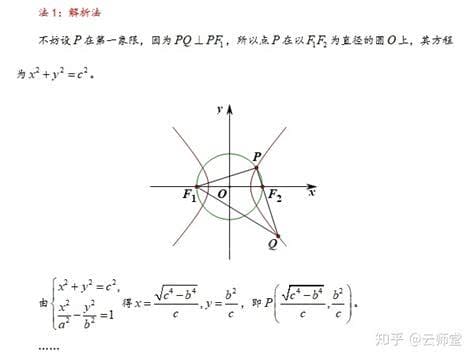
双曲线离心率所有公式

科普大全 2023-08-22 02:45:01

大家好，双曲线离心率所有公式小编来为大家解答。呢，很多朋友还不理解，现在让我们一起来介绍下，希望能帮助到你！

双曲线离心率所有公式

双曲线偏心率公式:在e=c/a的平面上，到给定点和直线的距离比是常数e((e>1)，即双曲线的偏心率)的点的轨迹称为双曲线。不动点称为双曲线的焦点，不动线称为双曲线的准线。双曲线准线的方程是(焦点在X轴上)或(焦点在Y轴上)。

特性

1.分支

从图中可以看出，双曲线有两个分支。当焦点在X轴上时，是左轴和右轴；当焦点在Y轴上时，就是上轴和下轴。

2.焦点

定义1中提到的两个不动点称为双曲线的焦点，定义2中提到的一个给定点也是双曲线的焦点。双曲线有两个焦点。焦点的水平(垂直)坐标满足c = a+b。

3.对齐

定义2中提到的给定直线称为双曲线的准线。

发展

双曲线路径公式

双曲线的路径是焦点和垂直于实轴的弦。有两条路径的长度为2b /a a..椭圆方程是

X/A+Y/B = 1，所以得到Y = B/A，正反两个直径的长度相加，所以是2b /a A..

路径长度

椭圆和双曲线的路径长度为| ab | = 2b ^ 2/a。

(其中A是长轴或实轴的1/2，B是短轴或虚轴的1/2，无论椭圆或双曲线的焦点在X轴还是Y轴，都可以得出这个结论)。

抛物线的路径长度为|AB|=4p。

(其中p是抛物线焦距的1/2)

在通过焦点的弦中，路径最短。

这个结论只适用于椭圆和抛物线，双曲线需要单独讨论。

如果双曲线的偏心率e >根号2，则实轴最短，即最短的焦点弦为2a。

如果双曲线的偏心率e=根号2，那么路径等于实轴，它们是最短的焦点弦。如果双曲线的偏心率θ> 0，

|MN|=2ab^2(k^2+1)/[(bk)^2+a^2]。

椭圆路径长度定理

椭圆的常见问题及解决方法

椭圆的路径长度定理是指椭圆的路径AB是垂直于长轴的直线与椭圆相交得到的线段AB。可以从勾股定理推导出来。椭圆中的路径是通过焦点的最短弦。

例如，有一个圆柱体，它被切割以获得横截面。证明是椭圆(第一种定义):

从圆柱体两端向中间挤压与圆柱体半径相同的两个半球，接触截面时停止。

然后你会得到两个公共点，显然它们是截面和球的切点。

设两点为F1和F2。

对于截面上的任意一点P，若过P的母线Q1和Q2为圆柱，球和柱的切线大圆分别与Q1和Q2相交，则PF1=PQ1，PF2=PQ2，所以PF1+PF2=Q1Q2。

根据定义1，截面是以F1和F2为焦点的椭圆。

同理，也可以证明圆锥体的斜截面(不穿过底部)是椭圆。