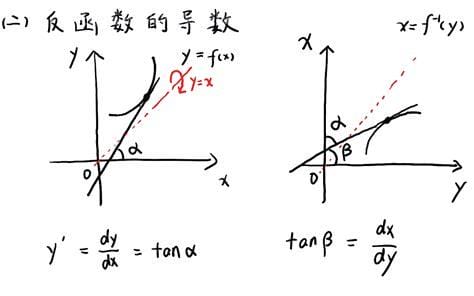
如何反函数求导，反函数的9种方法

科普大全 2024-01-07 16:24:01

最近很多朋友都遇到了如何反函数求导的问题，今天小编就来为大家解答，快来看看吧。

如何反函数求导，反函数的9种方法

求反函数的9种方法

只有一种方法可以找到反函数。就是反解方程，交换xy位置，求定义域。

要找到反函数:

1.利用反解方程，把X看成一个未知数，把Y看成一个已知数，求出X的值。

2.把这个公式中的x和y转换成位置，就得到反函数的解析式。

3.求反函数的定义域。

反函数也是函数，函数和它的反函数都是反函数，它们的定义和值域是互换的，对应的规律是互易的。一个函数及其反函数可以是两个不同的函数，也可以是同一个函数。

反函数定义:

一般来说，如果X和Y对应某个对应关系f(x)，y=f(x)，则y=f(x)的反函数为y=f-1(x)。反函数存在的条件是原函数必须一一对应(不一定在整个数域内)。

首先，判断反函数是否存在:

根据反函数存在定理，一个严格单调函数必有一个严格单调反函数，两个函数的单调性相同；

1.首先判断这个函数是否单调，如果不单调，那么它的反函数就不存在。

设y=f(x)的定义域为D，值域为f(D)。若将d中任意两点x和x视为x2，则判断函数与其反函数在相应区间内的单调性是否一致；

如果满足以上条件，反函数存在。

二、具体解决方案:

比如求y = x ^ 2的反函数。

X =根号y，那么f(x)的反函数就是正负根号x，求解后注意定义域和值域。反函数的定义域就是原函数的值域，反函数的值域就是原函数的定义域。

扩展数据:

反函数的存在定理

定理:一个严格单调函数必有一个严格单调反函数，两个函数的单调性相同。

在证明这个定理之前，先介绍函数的严格单调性。

设y=f(x)的定义域为D，值域为f(D)。如果对D中任意两点x1和x2，当x1