生活中的许多朋友最近问小编减法中哪个是减数哪个是被减数的问题,那么小编收集整合后,今天为大家分享关于的相关文章,一起来了解一下吧!一般来说,被减数-被减数=差。下面是一个例子。比如100-80=20,其中被减数是100,减数是80
2023-10-14 12:40:26

错位减法错位减法是数列常用的求和方法,应用于等比数列和等差数列的乘法运算。
举个例子,An=BnCn,其中Bn为等差数列,Cn为等比数列,分别列出Sn,然后将所有公式同时乘以等比数列的公比,即kSn错位一位,然后将两个公式相减。
比如sum Sn = x+3x+5x 2+7x 3+……+(2n-1)* x(n-1)(x≠0)。
当x=1时,Sn = 1+3+5+…+(2n-1)= n ^ 2。
当x不等于1时,Sn = 1+3x+5x 2+7x 3+…+(2n-1) * x (n-1)。
∴xsn=x+3x^2+5x^3+7x^4+…+(2n-1)*x^n
将两个表达式相减得到(1-x)sn = 1+2x[1+x+x2+x3+…+x(n-2)]-(2n-1)* x n。
简化为Sn =(2n-1)* x(n+1)-(2n+1)* x n+(1+x)/(1-x)2。
Sn= 1/2+1/4+1/8+....+1/2^n
同时将两边乘以1/2
1/2sn = 1/4+1/8+...+1/2 n+1/2 (n+1)(注意与原位置的区别,这样可以写得更清楚)。
两个表达式相减
1/2Sn=1/2-1/2^(n+1)
Sn=1-1/2^n
错位减法是求和的解题方法。在题型中:一般只有A之前的系数和A的指数相等时才能使用。这是一个例子(格式问题,a和n后面的数是指数):
s = a+2 a2+3 a3+……+(n-2)an-2+(n-1)an-1+nan(1)
在(1)的左右两边同时乘以a。等式(2)如下获得:
aS = a2+2 a3+3 a4+……+(n-2)an-1+(n-1)an+nan+1(2)
使用(1)-(2),等式(3)如下获得:
(1-a)S = a+(2-1)a2+(3-2)a3+……+(n-n+1)an-nan+1(3)
(1-a)S=a+a2+a3+……+an-1+an-nan+1
S = A+A2+A3+...+An-1+An用这个求和公式。
(1-a)S=a+a2+a3+……+an-1+an-nan+1
最后在方程两边同时除以(1-a),就可以得到s的通式。
相关文章

生活中的许多朋友最近问小编减法中哪个是减数哪个是被减数的问题,那么小编收集整合后,今天为大家分享关于的相关文章,一起来了解一下吧!一般来说,被减数-被减数=差。下面是一个例子。比如100-80=20,其中被减数是100,减数是80
2023-10-14 12:40:26
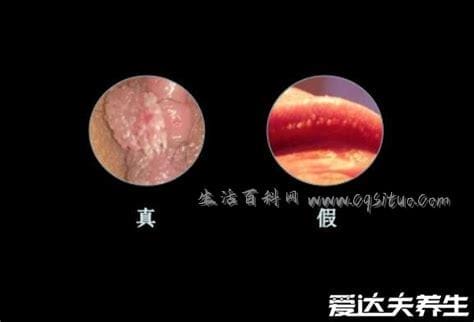
大家在生活的过程中会遇到很多问题,比如有些小伙伴对尖湿锐尤典型早期图片不是很懂,不过没有关系,小编今天就给大家详细讲解一下这个问题,具体内容如下。尖锐湿疣的潜伏期为1-6个月,一般为3个月。形状为丘疹状、乳头状、菜
2023-10-13 16:50:26

许多朋友不知道等比数列求和的极限怎么办,对此很疑惑,那么今天就和小编一起来看看吧,一定可以帮助到你。如果一个数列从第二项开始,每一项与前一项之比等于同一个常数,这个数列叫做几何级数。这个常数叫做几何级数的公比,通
2023-10-13 02:52:50

今天我想和大家分享一下关于啤酒花种植要求(啤酒花种植要求和条件)。以下是小编,对这个问题的总结。让我们来看看。今天给大家分享啤酒花种植要求的知识,也会讲解啤酒花种植的要求和条件。如果你碰巧解决了你现在面临的问
2023-09-30 06:13:01

有许多的朋友最近问小编心绞痛症状5个典型症状的问题,那么小编收集整合后,今天为大家分享关于的相关文章,一起来了解一下吧!心绞痛往往是由于冠状动脉供血不足、心肌缺血或缺氧引起的,这类问题发生时通常具有一定的特点。
2023-09-29 01:22:23