生活中,很多小伙伴不知道四种婚姻趁早离婚?今天小编针对这个问题做了这篇文章,详细内容我们来看一下。婚姻应该是永远不会幸福的,但如果遇到这四种婚姻,就会早早离婚,没有共同语言或感情,意见不合,一方会被家暴出轨,长期分居
2023-11-09 03:03:01
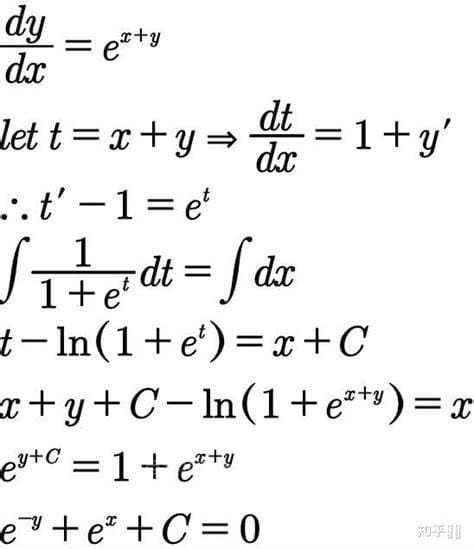
如何处理两体问题中交织的变量?分离变量法和交换关系的内在联系是什么?5月13日、15日中午12点,张朝阳物理课第53、54期播出。搜狐创始人、董事长兼CEO张朝阳坐在搜狐视频直播间里,用了两节课的时间讨论波函数在坐标空间的表示,研究两体问题中哈密顿本征方程的求解。通过选择合适的新变量和仔细推导,将两体运动方程分解为质心运动部分和相对运动部分。最后讨论了分离变量法与算子交换性的关系,阐明了算子交换性与算子公共本征态存在性的关系。
张朝阳在直播中介绍,在经典力学中,用粒子的位置和动量来描述物理系统,而在量子力学中,则用波函数来描述。波函数需要满足“单值、连续、归一化”的条件,可以作为矢量线性叠加得到其他波函数。所有物理波函数形成的线性空间称为希尔伯特空间。
经典力学中经常遇到的可观测量,如位置、动量、能量等。,成为量子力学中希尔伯特空间的线性算符。如果算符作用于波函数的结果与原波函数只相差一个比例系数,那么这个波函数称为算符的本征态,对应的比例系数称为这个本征态对应的本征值。波函数可以根据这些本征态展开,一个本征态展开系数的模平方,正好是观测者在观测波函数时获得相应本征值的概率。张朝阳在直播中不仅求解了动量本征态和坐标本征态,还将一般波函数展开为动量本征态和坐标本征态,发现坐标空间波函数在某一点的值的模平方就是在该点发现粒子的概率密度。
除了动量算符和坐标算符,哈密顿算符在量子力学中有着非常重要的作用,因为它出现在薛定谔方程中。张朝阳以一维空间的两体问题为例,展示了哈密顿算符的本征态和本征值的求解过程。两体问题哈密顿量中的势能项将两体的坐标耦合在一起,使得方程求解困难。因此选择质心坐标和相对坐标代替两体坐标作为波函数的自变量。进一步,通过复合函数导数的链式法则,两体坐标的偏导数可以表示为质心坐标和相对坐标偏导数的线性叠加。利用这些偏导数之间的关系,可以将哈密顿量分解为质心运动部分和相对运动部分之和。
然后把波函数写成变量分离的形式,代入哈密顿算符的本征方程,可以分解成两个独立的方程,一个是质心运动部分的本征方程,一个是相对运动部分的本征方程。分解后的特征值方程只有一个变量,相当于把原来复杂的两体问题变成了简单的单体问题,然后就可以求解特征值和本征值了。
(张朝阳用分离变量法求解哈密顿算符的本征方程)
很容易证明上面使用的变量分离形式的波函数是质心运动部分的哈密顿量和相对运动部分的哈密顿量的共同本征态。张朝阳证明了在简并的情况下,两个交换算符有一个共同的本征态。相反,如果两个算符的公共本征态能构成希尔伯特空间的完备基,那么它们就是可交换的。由此可见,质心运动的哈密顿量和相对运动的哈密顿量是倒易的,这说明如果要用分离变量的方法求解哈密顿量的本征方程,就需要把哈密顿量分解成倒易算符,通过求解这些倒易算符的相对简单的本征方程来求解原哈密顿量的本征方程,这正是我们用来求解氢原子薛定谔方程的方法。
到目前为止,《张朝阳的物理课》已经直播了五十多期。从去年11月第一节物理直播课开始,他首先从经典物理入手,普及牛顿运动定律。然后从经典物理的“两朵乌云”过渡到现代物理,讨论黑体辐射理论中的维恩公式和普朗克公式的知识。此后逐渐进入量子力学领域,从基本的薛定谔方程等理论内容,到氢原子的波函数,再到气体定容比热的温度梯度等更具体实际的情况。内容丰富,涉及面广,理论公式由浅入深,复杂与简单交融。
《张朝阳的物理课》直播风格独特:注重推导,通过详细的数学计算一步步推导出相关的物理公式,从头到尾把每一个公式都掩饰得清清楚楚。
据了解,《张朝阳的物理课》每周五、周日中午12点在搜狐视频直播。网友可在搜狐视频“关注流”搜索“张朝阳”观看直播及之前的完整视频播放;关注“张朝阳物理课”账号,查看课程“知识点”短视频;此外,还可以在搜狐新闻APP的“搜狐科技”账号上阅读每门物理课程的详细文章。
除了《张朝阳的物理课》,在直播方面,搜狐视频正在持续搭建知识直播平台,邀请各科学领域的头部主播直播科普知识。包括中国运载火箭技术研究院专家钱航现场讲述航天事业发展历程;北交大理学院老师陈正博士在线授课——《有趣的科学实验》;中科院基因组学博士、Metacode基因创始人田耕阐述了基因组学与生命的密切关系;天体物理学博士刘博阳博士普及“日全食是怎么来的”等等。未来会有更多的知识播报员进驻搜狐视频,一起互动,一起玩科普。
相关文章

生活中,很多小伙伴不知道四种婚姻趁早离婚?今天小编针对这个问题做了这篇文章,详细内容我们来看一下。婚姻应该是永远不会幸福的,但如果遇到这四种婚姻,就会早早离婚,没有共同语言或感情,意见不合,一方会被家暴出轨,长期分居
2023-11-09 03:03:01

生活中,很多小伙伴不知道大豆分离蛋白是什么东西?今天小编针对这个问题做了这篇文章,详细内容我们来看一下。最近经常听说人体最好补充一些大豆分离蛋白。这个大豆分离蛋白是什么东西有什么作用和效果?是一种蛋白质食品
2023-10-23 03:45:02
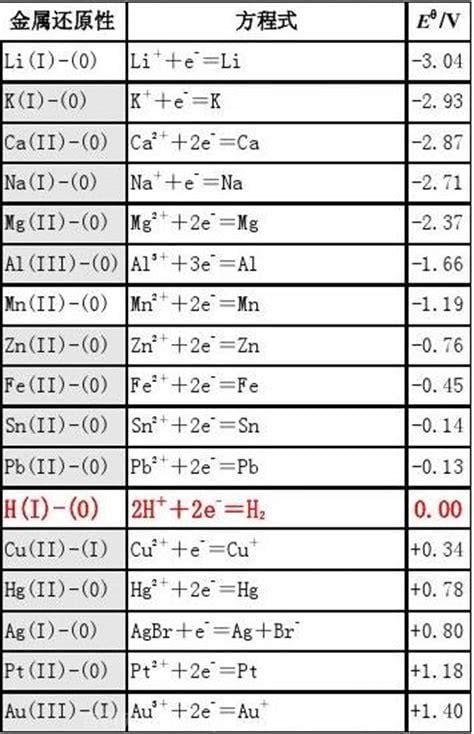
大家在生活的过程中总会遇到一些问题,比如标准电极电动势计算方程,那么今天小编就为大家分享关于的文章,希望在这篇文章中你能了解到相关内容。标准电动势计算公式:E=W/q(公式中,W代表电源将正电荷从负极移动到正极所做
2023-10-16 00:56:27

生活中很多小伙伴不了解氢氧化钙加化学方程式这件事,今天小编针对这个问题做了这篇文章,详细内容我们来看一下。氢氧化钙的化学式为Ca(OH)2,微溶于水,溶解度随着稳定性的增加而降低。澄清的石灰水称为氢氧化钙溶液。具有
2023-10-13 11:27:01
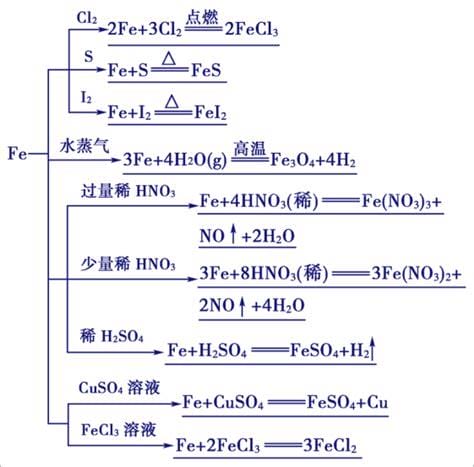
生活中,很多小伙伴不知道氧化铁与稀硫酸反应化学方程式,今天小编针对这个问题做了这篇文章,详细内容我们来看一下。氧化铁(Fe2O3)是金属氧化物,稀硫酸是硫酸(H2SO4)的水溶液,两者都是化合物,化合物之间发生复分解反应。当金
2023-10-13 08:36:01