多元回归分析(多元回归分析spss)

多元回归分析(多元回归分析spss)这个事情很多人都会遇见，对于带来的一些疑问也不少，就有很多小伙伴问小编具体是怎么回事？小编为此特意准备了这篇文章，目的是解决小伙伴们的问题，具体文章如下。

多元回归分析(多元回归分析spss) 序曲

刘桦/标题刘桦

韩愈

五月，石榴花开得正艳，枝头正在生长的时候，孩子们也开始成长了。

可惜这里没有车马，青苔颠倒。

这首诗的前两段正是时令，勾勒出五月石榴花的繁茂景象。后两期点明地点，说明石榴花不为游人所赏，故美无声散，委婉表达了诗人孤独的心境。全诗描写清新自然的景色，在描写客观景物中体现人生哲理。

这首诗的前两句描写山水，后两句抒发情怀。作者不直接写风景，而是通过人的感受，从侧面衬托出五颜六色的石榴花。但再美的花，也不寂寞，也不沉默。诗人感叹无人来赏花，是说他的朋友人才济济，却被统治者贬谪到穷乡僻壤，不能投入使用。“倒挂”二字，有力地批判了统治者对人才的无知，以及诗人和作家双方的怨恨。

多元线性回归分析简介

多元线性回归是一种研究多个变量之间线性相关性的统计分析方法。

在医学研究中，医学指标通常受多种因素影响，如年龄、性别、体重、劳动强度、饮食习惯、吸烟、饮酒、家族史等因素。回归方程可以用来描述一个因变量Y与多个自变量X1、X2、...，这就是所谓的多元线性回归。多元线性回归方程可总结如下:

其中，

y为因变量，是随机定量的观察值；x1,…..xp为p个自变量。β0 为常数项， β1 ……βp为回归系数。βj （j=1,2,3,….）表示在其他自变量固定不变的情形，自变量xj每改变一个单位时，其单独引起因变量y的评价变化量。ε为随机误差，也可称为残差，它是y的变化中不能用自变量解释的部分，服从正态分布。

在多元回归分析中，回归方程中对因变量Y的贡献不能直接与各变量的普通回归系数的数值进行比较，因此P个自变量的计量单位和变异性是不同的。有必要对原始数据进行标准化，即

然后用标准化数据拟合回归模型。此时，获得的回归系数表示为k1，k2，...kp，称为标准化偏回归系数和通径系数。标准化回归系数kj绝对值较大的自变量对因变量y的贡献较大。

多元回归分析的前提条件与一元线性回归的前提条件完全相同:直线表示线性、独立、正态、等方差。

自变量选择方法

因为在多元回归分析中，自变量有多个自变量，有时需要进行筛选，包括向前法、向后法和逐步回归法。相应的方法在前面的章节中已经解释过了。

SPSS实现多元线性回归

例:已知27例糖尿病患者血清总胆固醇、甘油三酯、空腹胰岛素、糖化血红蛋白、空腹血糖的测定值，分析血糖与其他指标关系的回归方程。

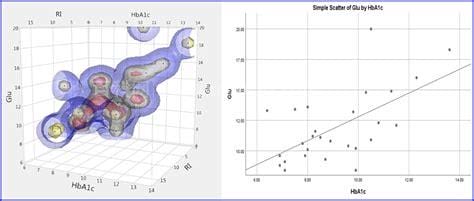
1.线性关系的验证

做散点图矩阵：分析—图形—散点图／点图，选择矩阵散点图，将4个变量放入变量框，点击"确定" 从下图可看出，血糖与指标之间存在一定的线性关系

2.开放分析-回归-线性

3.参数选择

(1)主页描述

如下图所示，将 血糖 放入因变量框，其他四个变量为自变量，方法选择 步进法。

(2 )"统计"页面

选择 估算值、模型拟合、R方变化量、德宾-沃森、个案诊断、共线性诊断

(3)"图"页

将 标准化残差（ZRESID）放入Y 轴框，标准化预测残差（ZPRED）放入X 轴框，同时勾选残差直方图和正态概率图。此步目的是验证残差是否正态，反映Y 是否独立。

(4)"保存"页面

选择 未标准化值、单值，如下图所示

(5 )"选项"页面

保持默认选项，如下图所示

4.结果的输出和解释:

(1)模型筛选过程

模型1用逐步法选择了 X4.糖化血红蛋白，然后模型2用逐步法选择了 X1.总胆固醇，X4.糖化血红蛋白 仍保留在模型2中，另外两个变量没有达到选择标准，最终没有进入。表格的右侧注明相应的筛选方法和选择及剔除标准。

(2)模型总结

下图给出了拟合的两个模型决定系数的改变情况，从调整R方来看，随着变量 X1.总胆固醇的进入，模型2可解释的变异占总变异比例比模型1增加不少。

(3)方差分析表

方差分析反映了模型整体的显著性，由下表可知，两个模型的P=0.000<0.05，构建的回归模型有统计学意义。但模型有统计学意义不等于模型内所有变量就用统计学意义，还需进一步对各自变量进行检验。

(4)回归系数

下表是两个模型中各个系数检验的结果，用的是t检验。从结果可看出，模型2中两个自变量的系数都有统计学意义。X4.糖化血红蛋白的 未标准化系数为 0.732，标准化系数为 0.456；X1.总胆固醇的未标准化系数为0.678，标准化系数为0.369。通过比较两个变量的标准化回归系数的绝对值，可知X4.糖化血红蛋白对 血糖 的贡献较大。最终的回归方程为：

Y=1.310+0.732*X4。糖化血红蛋白+0.678*X1。总胆固醇。

(5)排除变量的解释

下表反映了拟合模型过程中没有进入模型的变量的检验情况。

(6)标准化残差图

可见总体上残差符合 正态分布。说明符合线性回归的 正态性的条件

(7)残差散点图

为回归标准化残差与标准化预测值的散点图，基本在+3个标准差以内，说明总体效果较好，满足等方差性。

5.语法

* * * * * * * * * * * * * * * * * *散点图矩阵* * * * * * * * * * * *。图表/散点图(矩阵)= 1x2x3x4 y/missing = listwise。* * * * *.。回归/缺失列表/统计系数输出R ANOVA COLLIN TOL CHANGE/CRITERIA = PIN(. 05)POUT(. 10)CIN(95)/NOORIGIN/DEPENDENT Y/METHOD =逐步X1 X2 X3 X4/散点图=(*ZRESID，* z PRED)/残差杜宾直方图(ZRESID)/norm prob(z resid)/case wise图(z resid)异常值(3)/保存PRED ICIN。